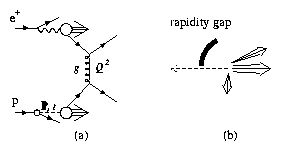25.0cm -1.5cm 17.0cm -0.8cm GLAS-PPE/96-03June 17, 1996 Rapidity Gaps in Hard Photoproduction

Rapidity Gaps in Hard Photoproduction

L.E. Sinclair¹
for the ZEUS Collaboration Talk presented at the Topical Conference on Hard Diffractive Processes,
Eilat, Israel, February 1996.

Abstract

Recent results obtained from studies of diffractive processes in hard photoproduction performed by the ZEUS collaboration using data delivered by HERA in 1993 and 1994 are presented. In particular, we have found that (7 ą3)% of events with two jets at a pseudorapidity interval of 3.5 to 4 are inconsistent with a non-diffractive production mechanism. These events may be interpreted as arising due to the exchange of a colour singlet object of negative squared invariant mass (-t) around 40 GeV². We have also probed the structure of the exchanged colour singlet object in low-t diffractive scattering. By comparing the results from photoproduction and electroproduction processes we find that between 30% and 80% of the momentum of the exchanged colour singlet object which is carried by partons is due to hard gluons.

1. Introduction

In this first section a brief introduction to hard photoproduction is presented. Then the general characteristics of the photoproduction events which give rise to rapidity gaps in the final state are described and diffraction is defined in this context. The events may be classified into two groups, those which give rise to a central rapidity gap, and those which give rise to a forward rapidity gap. The results which have been obtained by the ZEUS Collaboration from the study of these two classes of events are presented and discussed in the following two sections. These are published results [1,2], and the reader is referred to the publications for detailed accounts of the event selection, the Monte Carlo event generation and the corrections for detector effects. Some concluding remarks and an outlook are provided in the final section.

1.1 Hard photoproduction

The canonical HERA event proceeds as illustrated in Figure 1(a). The incoming positron is scattered through a large angle exchanging a photon probe of (negative) virtuality as high as Q² ~ 5 ·10⁴ GeV². The structure of the proton may be studied down to values of the Bjorken-x_p variable as low as x_p ~ 5 ·10^-3.

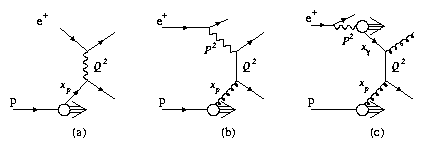
Figure 1: Diagrams showing HERA processes. The canonical electroproduction process is shown in (a). A leading order direct photoproduction process is shown in (b) while an example of a leading order resolved photoproduction process is shown in (c). Of course the electroproduction cross section is strongly peaked to Q² ~ 0 and the events most copiously produced at HERA are soft photoproduction events. However photoproduction events which lead to the production of high transverse energy jets in the final state are also characterized by a large (negative) squared momentum transfer Q². An example is shown in Figure 1(b). For these hard photoproduction events the negative of the squared invariant mass of the photon is denoted P² and of course, P² ~ 0. Again, very low values of x_p of the proton may be probed and note that the photoproduction processes (in contrast to the electroproduction processes) are directly sensitive to the gluon content of the proton.

The incoming photon may fluctuate into a hadronic state before interaction with the proton. This situation is illustrated in Figure 1(c). The momentum fraction variable x_g has been introduced, where x_g represents the fraction of the photon's momentum which participates in the hard interaction. The class of events represented by Figure 1(b) are known as direct photoproduction events and have x_g = 1. Resolved photoproduction events are represented by Figure 1(c) and have x_g < 1. The present discussion is clearly limited to leading order processes although a definition of x_g may be made which is calculable to all orders and allows for a well defined separation of direct and resolved photoproduction processes [3].

A hard photoproduction event in the ZEUS detector is shown in Figure 2. In the z - R display on the left-hand side the positrons approach from the left and the protons from the right. The e⁺ beam has an energy of 27.5 GeV and the p beam has an energy of 820 GeV. The calorimeter is deeper in the ``forward'' or proton direction, to cope with this asymmetry in the beam energies. This proton direction is the direction of positive pseudorapidity, h = -lntan(J/ 2), where J is the polar angle with respect to the p beam direction.

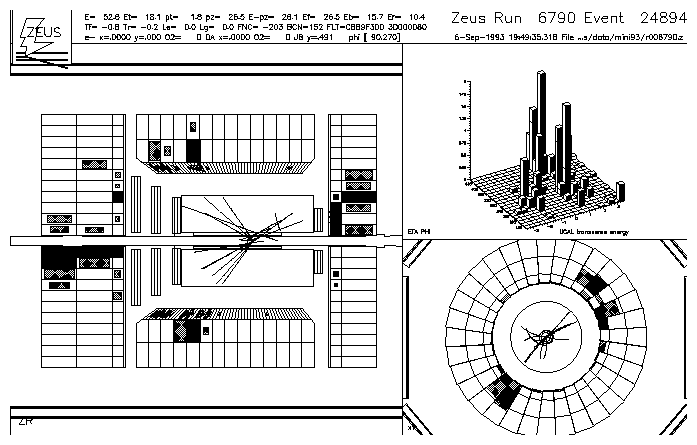
Figure 2: A hard photoproduction event in the ZEUS detector. The z -R longitudinal view is shown on the left hand side. In the upper right hand corner the h and f coordinates of the hit calorimeter cells are shown, weighted by their transverse energies. In the lower right hand corner the x - y or transverse view is shown. Two jets of large transverse energy are measured in the tracking chambers and the calorimeter and are clearly apparent in all three views. The jets are both at h ~ 1 (J ~ 40^°) and are back to back in f. It is the energy deposits and tracks of these jets which we use to select a sample of hard photoproduction events. Notice that there is a large energy deposit in the far-forward region next to the beam pipe. This energy is associated with the proton remnant. There is also a large energy deposit in the rear direction which could be called the photon remnant if this were considered a resolved photon event. (The transverse energy of the rear jet in this particular event is actually sufficiently large that it may be appropriate to consider this a higher order direct photoproduction event.) Notice that there is no energy deposit which could be associated with the scattered e⁺, which is lost down the rear beam pipe in photoproduction processes.

1.2 Diffraction

The analyses which will be discussed in this report both make use of the operational definition of diffraction [4]:

A process is diffractive if and only if there is a large rapidity gap in the produced-particle phase space which is not exponentially suppressed.

They are, in addition, studies of hard diffraction in the sense that the events all possess a large (negative) squared momentum transfer, Q², or a high energy scale, Q. The hard diffraction events are further subdivided into two classes both of which have gone by a number of different names.

The first class of events may be called hard diffractive scattering, hard double-dissociation diffraction or high-t diffraction. They proceed as shown in Figure 3(a), via the exchange of a colour singlet object of large negative squared invariant mass, t. (t, in both event classes, refers to the square of the momentum transfer across the exchanged colour singlet object. This object is called a pomeron and denoted IP.)

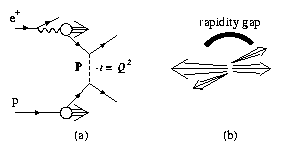
Figure 3: Hard diffractive scattering at HERA. The diagram for this process is shown in (a). The exchanged colour singlet object is denoted IP and the negative of its squared invariant mass, -t, sets the energy scale of the interaction, (Q = \protect[Ö(-t)]). In the final state, shown in (b), there are two high transverse energy jets and two remnant jets with a gap in particle production in the central rapidity region. Owing to the absence of colour flow across the middle of the event a gap in the production of particles is expected to be observable. These events thus contain a central rapidity gap as illustrated in Figure 3(b). This may be contrasted with the situation, for example, where a gluon is exchanged in place of the pomeron in Figure 3(a). Central rapidity gap events will be examined in Sect. 2.

The second class of events has been called diffractive hard scattering, hard single-dissociation diffraction and low-t diffraction. These events are understood to occur when a colour singlet object, travelling collinearly with the proton, is probed by the hard subprocess. An example is shown in Figure 4(a).

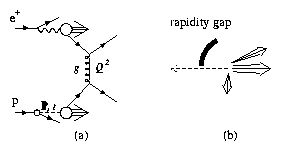
Figure 4: The diffractive hard photoproduction process at HERA is shown in (a). The pomeron, denoted IP, is shown being emitted from the proton with a squared momentum transfer t. A quark from the pomeron subsequently enters the hard subprocess which is mediated by the exchange of a gluon, denoted g, and characterized by the energy scale Q. The topology of the final state is shown in (b). There are two high transverse energy jets associated with the hard subprocess. There may be a photon remnant. However the proton is not broken up and disappears down the forward beam pipe leaving a gap in particle production at high rapidities. Because the object emitted by the proton does not carry colour, particle production into the forward, or high-h, region of phase space is suppressed. This process thus leads to the formation of a forward rapidity gap as illustrated in Figure 4(b). This process is studied in Sect. 3.

2. Central Rapidity Gaps

The results discussed in this section have been published in [1]. We have isolated a sample of hard photoproduction events containing at least two jets of transverse energy E_T^jet > 6 GeV. The jets are found using a cone algorithm with jet cones of radius 1 in h- f space. The pseudorapidity interval between the jet centres, Dh, exceeds 3.5 in 535 of the 8393 events. Note that to leading order Dh = ln([^s] / -[^t]) where [^s] and [^t] are the usual Mandelstam variables of the hard subprocesses. Dh> 3.5 therefore means that [^s] > 30 ·- [^t] which falls into the Regge regime, [^s] >> - [^t].

Gap candidate events are defined as those which have no particles of E_T^particle > 300 MeV between the edges of the jet cones in pseudorapidity. The size of the gap therefore lies between Dh and Dh-2R = Dh-2.

An event from this sample is shown in Figure 5.

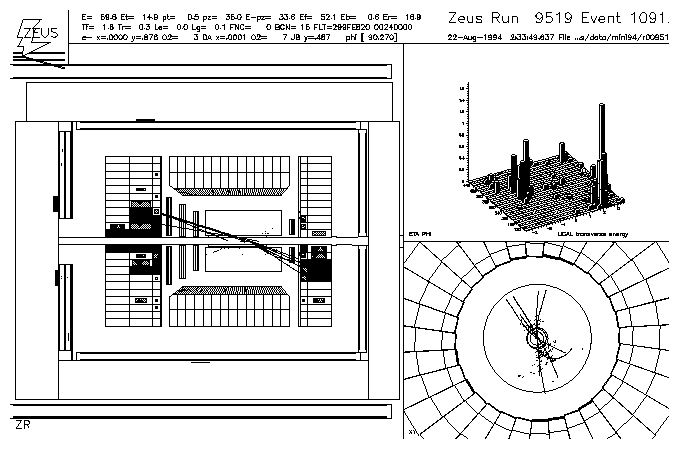
Figure 5: A hard photoproduction event with a central gap in the ZEUS detector. The z-R view of the ZEUS detector is shown on the left side. The lego plot of the E_T weighted energy deposits in the calorimeter versus their h and f is shown in the upper right picture and the lower right picture shows the x-y cross section through the ZEUS detector. There are two high transverse energy jets in this event which are back to back in f and have a pseudorapidity interval of Dh = 3.6. There are additional energy deposits around the forward beam pipe which correspond to the proton remnant and energy deposits near the rear beam pipe which may be associated with the photon remnant. This is in fact a gap candidate event. There are no candidate particles in the pseudrapidity interval between the jet cones having a transverse energy of E_T^particle > 300 MeV. There are, however, some very low energy energy deposits in this region which could in some cases be due to calorimeter noise. Alternatively they may be particles which are so soft that they have no memory of their parent parton's direction. The E_T^particle threshold is a necessary theoretical tool [5,6,7] as well as a convenient experimental cut.

The characteristics of this event sample are illustrated in Figure 6. Here the data are shown uncorrected for any detector effects, as black dots. The errors shown are statistical only. The data are compared to predictions from the PYTHIA [8,9] generator for hard photoproduction processes. These predictions have been passed through a detailed simulation of the selection criteria and of the detector acceptance and smearing.

Figure 6: Sample characteristics. Errors are statistical only. No correction for detector effects has been performed. Monte Carlo simulated events have been subjected to full detector simulation. (a) Jet profile. Data are shown as black dots and PYTHIA standard hard photoproduction processes are shown as the solid line. (b) The Dh distribution. Data are shown as black dots, the PYTHIA standard sample is shown by the open circles and the PYTHIA sample containing 10% of photon exchange processes is shown by the stars.

Figure 6(a) shows the average profile of the two highest E_T^jet jets. In the jet profile, dh^cell = h^cell - h^jet of each calorimeter cell is plotted, weighted by the cell transverse energy, for cells with |f^cell - f^jet| less than one radian. The data show good collimation and a jet pedestal which increases gradually towards the forward direction. The PYTHIA prediction for the standard direct and resolved hard photoproduction processes is shown by the solid line for comparison. The description is reasonable, however there is a slight overestimation of the amount of energy in the jet core and underestimation of the jet pedestal. Higher order processes and secondary interactions between photon and proton spectator particles are neglected in this Monte Carlo simulation. It is anticipated that their inclusion could bring the prediction into agreement with the data [10,11]. Notice that, naïvely, this discrepancy would be expected to give rise to proportionally fewer events containing a rapidity gap in the data than in the Monte Carlo sample.

Figure 6(b) shows the magnitude of the pseudorapidity interval between the two highest transverse energy jets, Dh. The number of events is rapidly falling with Dh but we still have a sizeable sample of events with a large value of Dh. This distribution is well described by the standard PYTHIA simulation of photoproduction events which is here represented by open circles. The stars show a special PYTHIA sample which has been introduced in this analysis primarily for the purpose of obtaining a good description of the data and understanding detector effects. 90% of this sample is due to the standard photoproduction processes. The other 10% of this sample is due to quark-quark scattering via photon exchange (Figure 3(a) with the IP replaced by a g) and obviously this 10% contains no contribution from leading order direct photoproduction processes. (Note that 10% is about two orders of magnitude higher than one would obtain from the ratio of the electroweak to QCD cross sections.) The combined Monte Carlo sample also provides a good description of the Dh distribution.

We define the gap-fraction, f(Dh), to be the fraction of dijet events which have no particle of E_T^particle > 300 MeV in the rapidity interval between the edges of the two jet cones. The gap-fraction, uncorrected for detector effects, is shown in Figure 7. The data are shown as black dots, the events from the standard PYTHIA simulation are shown as open circles and the events from the PYTHIA simulation containing 10% photon exchange processes are shown as stars. The errors are statistical only. A full detector simulation has been applied to the Monte Carlo event samples.

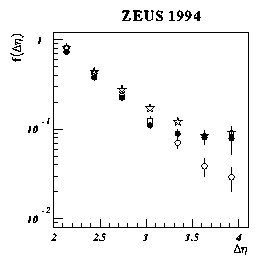
Figure 7: The distribution of the fraction of events containing a gap, f(Dh), with respect to Dh. The black dots represent the data, the open circles represent the standard hard photoproduction simulated events and the stars represent the simulated event sample of which 10% is due to photon exchange processes. The errors are statistical only, no correction for detector effects has been made, and the Monte Carlo samples have been passed through a detailed simulation of the ZEUS detector acceptance and smearing. A comparison of the gap-fractions for data and Monte Carlo events in Figure 7 reveals an excess in the fraction of gap events in the data over that expected for standard hard photoproduction processes. Additionally, the data exhibit a two-component behaviour. There is an exponential fall at low values of Dh, but there is little or no dependence of f(Dh) on Dh for Dh> 3.2. We recall the definition of diffraction proposed in Sect. 1.2. One is tempted to interpret the exponential fall of f(Dh) as being due to the production of gaps in non-diffractive processes. Then the flat component which dominates the rate of rapidity gap event production at large Dh may be naturally interpreted as arising from a diffractive process. However we must check first that this two-component behaviour of f(Dh) survives a full correction for detector acceptance and smearing. A detailed description of the correction method and the assignment of systematic errors may be obtained elsewhere [1,12].

The measured gap-fraction, corrected for detector effects, is shown in Figure 8 (black dots). The statistical errors are shown by the inner error bar and the systematic uncertainties combined in quadrature with the statistical errors are indicated by the outer error bars. (The data are the same in Figures 8(a) and (b).)

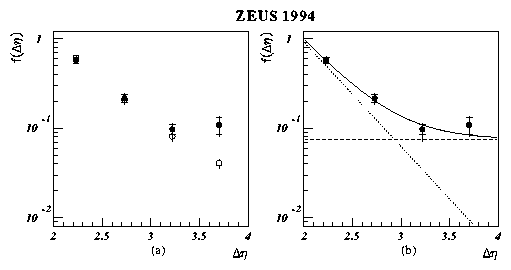
Figure 8: Corrected gap-fraction. The data are shown as black dots. The inner error bar shows the statistical error and the outer error bar shows the systematic uncertainty combined in quadrature with the statistical error. The open circles in (a) show the expectation from PYTHIA for standard hard photoproduction processes. The solid line in (b) shows the result of a fit to an exponential plus a constant dependence where the dotted and dashed lines show the exponential and constant terms respectively. Although there is some migration of events the overall detector corrections do not significantly affect the gap-fraction.

The corrected gap-fraction is compared with the prediction of the PYTHIA Monte Carlo program for standard hard photoproduction processes in Figure 8(a). (The PYTHIA prediction is shown by the open circles.) There is a significant discrepancy between the data and the prediction in the bin corresponding to Dh> 3.5. If we let the Monte Carlo prediction represent our expectation for the behaviour of the gap-fraction for non-diffractive processes then we can obtain an estimate of the diffractive contribution to the data by subtracting the Monte Carlo gap-fraction from the data gap-fraction. We obtain .07 ą.03. Therefore we estimate that 7% of the data are due to hard diffractive processes.

In Figure 8(b) a second method of estimating the contribution from diffractive processes is illustrated. Here we have made direct use of the definition of diffraction quoted in Sect. 1.2. We have performed a two-parameter c² fit of the data to the sum of an exponential term and a constant term, constraining the sum to equal 1 at Dh = 2. (Below Dh = 2 the jet cones are overlapping in h.) The diffractive contribution which is the magnitude of the constant term is thus obtained from all four of the measured data points. It is 0.07 ą0.02(stat.) ^+0.01 _-0.02(sys.) or again, 7% of the data are due to hard diffractive processes.

A caveat is in order. Implicit in both methods of estimating the fraction of diffractive processes in the data is the assumption that exactly 100% of hard diffractive scatterings will give rise to a rapidity gap. In fact this is considered to be an overestimate. Interactions between the g and p spectator particles can occur which would fill in the gap. Therefore the result of 0.07 ą0.02(stat.) ^+0.01 _-0.02(sys.) should be interpreted as a lower limit on the fraction of hard diffractive processes present in the data.

The probability of no secondary interaction occurring has been called the gap survival probability [13]. Estimates for the survival probability in pp interactions range between 5% and 30% [13,14,15]. However for these gp collisions we expect the survival probability to be higher due (in part) to the high values of x_g of this data sample compared to typical values of x_p in a pp data sample.² Therefore we do not consider the ZEUS result to be incompatible with the D0 result, 0.0107 ą0.0010(stat.) ^+0.0025_-0.0013(sys.) [16], and the CDF result, 0.0086 ą0.0012 [17].

In summary, ZEUS has measured the fraction of dijet events which contain a rapidity gap between the jets, f(Dh). From a comparison of the uncorrected f(Dh) with that obtained from the PYTHIA simulation of hard photoproduction processes (with full detector simulation) we conclude that the data are inconsistent with a completely non-diffractive production mechanism. From the behaviour of the fully corrected f(Dh), we determine that the hard diffractive contribution to the dijet sample is greater than (7 ą3)%. This value is obtained for two different methods of estimating the non-diffractive contribution, i) letting the non-diffractive contribution be represented by the PYTHIA prediction for hard photoproduction processes and ii) obtaining the non-diffractive contribution directly from an exponential fit to the data.

3. Forward Rapidity Gaps

The class of events which will be discussed in this section exhibits a rapidity gap extending to high values of h. An example is shown in Figure 9.

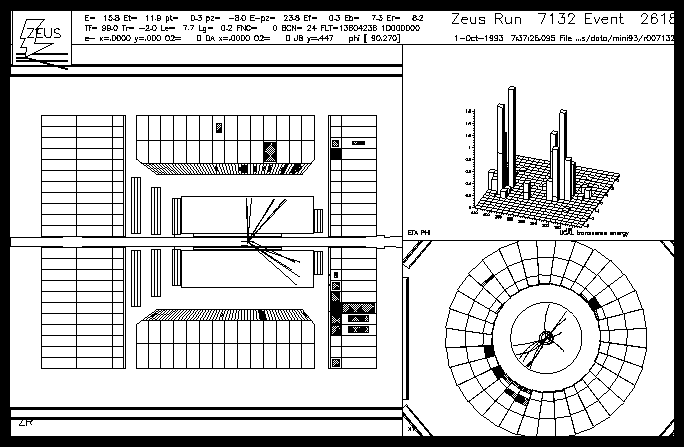
Figure 9: A hard photoproduction event with a foward gap. The z-R display of the ZEUS detector is shown on the left hand side. In the upper right hand corner the h and f coordinates of the calorimeter energy deposits are shown, weighted by their transverse energy. The lower right hand view is the x-y cross section. There are two high transverse energy jets which are back to back in f and no scattered e^- candidate. This is a hard photoproduction event. However there is no energy in the forward direction around the beam pipe which could be associated with the fragmentation products of the proton remnant. This is, therefore, a candidate diffractive hard scattering event.

This analysis proceeds in a similar way to that described in the previous section. First the uncorrected data are compared to Monte Carlo generated event samples which have been subjected to a full simulation of the ZEUS detector. In a second step the generated event samples are used to correct the data for the effects of the detector smearing and acceptance. Again, specific details of the analysis should be obtained from the publication [2].

The diffractive hard scattering process is understood to proceed as illustrated in Figure 10(a) where we have introduced two new momentum fraction variables. x_IP represents the fraction of the proton's momentum which is carried by the pomeron and b represents the fraction of the pomeron's momentum which is carried into the hard subprocess. Of course x_IP ·b gives the familiar Bjorken-x_p variable.

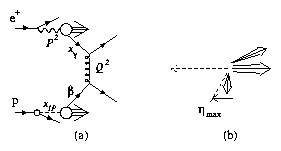
Figure 10: Kinematics of the diffractive hard photoproduction process. The meaning of the momentum fraction variables x_IP and b is illustrated in (a) where the fraction of the photon's momentum entering the hard subprocess, x_g, the photon virtuality, P², and the squared momentum transfer which sets the energy scale of the hard subprocess, Q², are also indicated. The pseudorapidity of the particle with the highest pseudorapidity is denoted h_max as illustrated in (b). The other important variable for describing the diffractive hard photoproduction process is h_max. h_max is defined to be the pseudorapidity of the most forward going particle (measured using the calorimeter) which has energy exceeding 400 MeV. The definition of h_max is illustrated schematically in Figure 10(b).

The h_max distribution for a sample of hard photoproduction events is shown in Figure 11. For this particular plot a subsample of events is shown for which the total hadronic invariant mass, M_X, (measured using all of the energy deposits in the calorimeter) satisfies M_X < 30 GeV. The data are shown by black dots and are not corrected for detector effects. The errors shown are statistical only. The data are peaked toward a value of h_max which is close to the edge of the calorimeter acceptance. However there is a large contribution

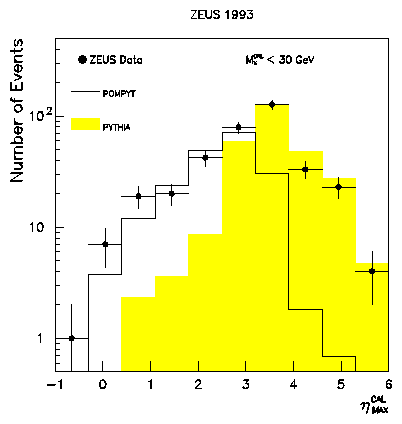
Figure 11: The h_max distribution for a sample of hard photoproduction events. The data are shown by black dots with error bars representing statistical errors only. No corrections for detector effects have been made. The shaded histogram shows the prediction from the PYTHIA standard hard photoproduction events. The open histogram shows the prediction from the POMPYT simulation of gIP scattering where the IP contains a hard gluon spectrum (see text). The Monte Carlo event samples have been subjected to a full simulation of the detector acceptance and smearing. from events with very low values of h_max, indicating the presence of a forward rapidity gap. Also shown in this figure are two Monte Carlo predictions which include a full simulation of the ZEUS detector. The shaded histogram shows the PYTHIA prediction for standard hard photoproduction processes. It fails to describe the large rapidity gap events of the data which occur at low values of h_max. To describe these large rapidity gap events we must introduce the Monte Carlo program POMPYT [18], the prediction of which is shown by the open histogram.

POMPYT is a Monte Carlo implementation of the Ingelman-Schlein model [19] which assumes that the hard photoproduction cross section s^jet_gp factorizes in the following way.

s^jet_gp = f_{IP / p}(x_IP,t) Ä f_{a / IP}(b, Q²) Ä

^
s

(

^
s

,Q²).

(1)

In words, the jet cross section, s^jet_gp, may be written as the convolution of a term representing the flux of pomerons in the proton, f_{IP / p}(x_IP,t), with a term describing the flux of partons in the pomeron, f_{a / IP}(b, Q²), and with the subprocess cross section, [^(s)]([^s],Q²). The direct photoproduction subprocess cross section includes only the hard subprocesses, gq Ž q g and gg Ž q q. In resolved photoproduction it includes in addition to the hard subprocesses qq Ž qq, qg Ž qg, etcetera, the flux of partons in the photon, f_{a / g}(x_g,Q²). The hard subprocess cross sections are calculable in perturbative QCD and some experimental information exists which constrains the f_{a / g}(x_g,Q²). Therefore [^(s)]([^s],Q²) is a known input in Eqn. 1. The pomeron flux factor, f_{IP / p}(x_IP,t), may be determined using Regge inspired fits to hadron-hadron data. The remaining unknown ingredient is the pomeron structure. We neglect the energy scale dependence of f_{a / IP}(b, Q²) and consider two extreme possibilities for its b dependence. The first, bf_{a / IP}(b) = 6 b(1 - b), yields a mean IP momentum fraction of ábń = 1 / 2 and is therefore known as the hard parton density. The second, bf_{a / IP}(b) = 6 (1 - b) ⁵, has ábń = 1 / 7 and is called the soft parton density. Finally, it is not clear whether there should be a momentum sum rule for the pomeron, that is, whether S_IP ş ň₀¹ dbĺ_a bf_{a / IP}(b) must equal 1 or not.

The open histogram in Figure 11 shows the POMPYT prediction for a IP consisting entirely of gluons with the hard momentum spectrum. A fairly satisfactory description of h_max may be achieved. In addition the POMPYT prediction is able to describe the M_X distribution, and the distribution of the photon proton centre-of-mass energies, W_gp, for rapidity gap events with h_max < 1.8. (The results are similar for a IP composed entirely of hard quarks.) For this reason we say that the data are consistent with containing a contribution from diffractive hard photoproduction processes.

In the second step of the analysis we correct the data for all effects of detector acceptance and smearing. We present in Figure 12 the ep cross section for photoproduction of jets of E_T^jet > 8 GeV as a function of the jet pseudorapidity. This cross section is for events which have a rapidity gap characterized by h_max < 1.8.

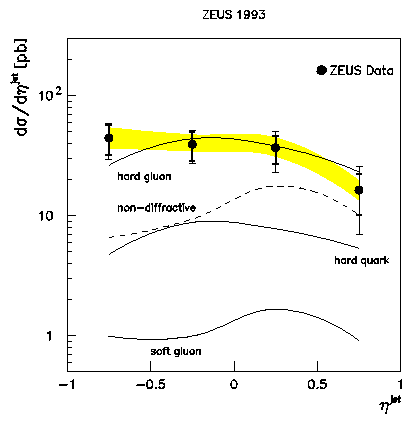
Figure 12: Cross section d s/ d h^jet for photoproduction of jets with E_T^jet > 8 GeV in events with h_max < 1.8. The inner error bars show the statistical errors and the outer error bars the systematic uncertainty added in quadrature - excluding the systematic uncertainty due to the calorimeter energy scale which is shown by the shaded band. The PYTHIA prediction for standard hard photoproduction processes is shown by the dashed line. The POMPYT predictions ds^{hard gluon}/dh^jet, ds^{hard quark}/dh^jet and ds^{soft gluon}/dh^jet for diffractive hard processes with different parton distribution functions and S_IP = 1 are shown by the solid lines. The PYTHIA prediction for this cross section for non-diffractive processes is shown by the dashed line. It is too low in overall magnitude to describe the data as well as being disfavoured in shape. The POMPYT predictions, ds^{hard gluon}/dh^jet, ds^{hard quark}/dh^jet and ds^{soft gluon}/dh^jet for the hard gluon, the hard quark and the soft gluon pomeron parton densities respectively where S_IP = 1 are shown by the solid curves. The soft parton density very rarely gives rise to sufficient momentum transfer to produce two E_T^jet > 8 GeV jets and so ds^{soft gluon}/dh^jet lies far below the cross sections for the hard parton densities in overall normalization. ds^{soft gluon}/dh^jet is inconsistent with the data in overall magnitude as well as being disfavoured in shape. We do not consider soft parton densities further. ds^{hard quark}/dh^jet is consistent with the data in shape but too small in magnitude. ds^{hard gluon}/dh^jet is capable of describing both the shape and magnitude of the measured cross section. Note, however, that the non-diffractive contribution to the data has not been subtracted, nor has the double dissociation contribution.

In the final stage of the analysis the non-diffractive contribution was subtracted from the data using the PYTHIA prediction (which has been shown to provide a good description of inclusive jet cross sections in photoproduction [20]). A contribution of (15 ą10)% due to double dissociation processes was also subtracted. Then the assumption that S_IP = 1 was relaxed. The IP was assumed to be composed of a fraction c_g of hard gluons and a fraction 1-c_g of hard quarks. Then for various values of c_g the expression S_IP · [ c_g ·ds^{hard gluon}/dh^jet + (1-c_g) ·ds^{hard quark}/dh^jet ] was fit to the measured ds/ dh^jet distribution to obtain S_IP. (The POMPYT predictions for ds^{hard gluon}/dh^jet and ds^{hard quark}/dh^jet were used in the fit.) The result of this series of fits is shown in Figure 13 by the solid line where the statistical uncertainty of the fit is indicated by the shaded band.

Figure 13: Allowed regions of the S_IP - c_g plane. The solid line and its shaded band of uncertainty show the constraint from the measurement of ds/ dh^jet. The dash-dotted lines and their shaded band of uncertainty show the constraint imposed from the measurement of F₂^D(3). (The upper dash-dotted curve is for two quark flavours and the lower dash-dotted curve is for three quark flavours.) We find, for instance, that the data are do not favour a IP which consists exclusively of hard gluons and simultaneously satisfies the momentum sum rule, S_IP = 1. (See [2], however, for a discussion of additional theoretical systematic uncertainties.)

Results from studies of diffractive hard electroproduction have been expressed in terms of the diffractive structure function, F₂^D(3)(b,Q²,x_IP) [21,22]. The expression of factorization is then, F₂^D(3)(b,Q²,x_IP) = f_{IP / p}(x_IP) · F₂^IP(b,Q²). Integrating this over x_IP and b and then subtracting the integral over the pomeron flux thus gives the sum of the momenta of all of the quarks in the pomeron, S_IP ·(1 - c_g). The ZEUS measurement [22], S_IP ·(1 - c_g) = 0.32 ą0.05, is shown in Figure 13 by the lower dot-dashed line. This is the result for two flavours of quark in the IP. The result for three flavours of quark is S_IP ·(1 - c_g) = 0.40 ą0.07, the upper dot-dashed line in Figure 13. The dark-shaded band shows the additional measurement uncertainty.

Assuming that the pomeron flux is the same in the measurement of F₂^D(3) and of ds^jet/dh^jet(h_max < 1.8) one can combine the two analyses to determine the allowed ranges, 0.5 < S_IP < 1.1 and 0.35 < c_g < 0.7. However the S_IP range is affected by additional uncertainties in the normalization of the pomeron flux factor. Taking into account all remaining systematic uncertainties of the measurements we find 0.3 < c_g < 0.8. This measurement is independent of the pomeron flux and of the total momentum carried by partons in the pomeron.

In summary, the distributions of h_max, M_X and W_gp indicate that the events with a forward rapidity gap are consistent with a diffractive hard scattering via exchange of a low-t pomeron. The ep cross section ds/dh^jet for the photoproduction of jets of E_T^jet > 8 GeV in large rapidity gap events (h_max < 1.8) has been measured and is significantly larger than the cross section due to non-diffractive processes. A comparison of the ds/dh^jet measurement in photoproduction with the measurement of F₂^D(3) in electroproduction indicates that 30% to 80% of the momentum of the pomeron which is due to partons is carried by hard gluons.

4. Conclusions and Outlook

Evidence is being accumulated which indicates that there is a strongly interacting colour singlet object which can mediate high-t interactions and which also contributes through its partonic content to low-t interactions. Further work to extrapolate the diffractive cross section to intermediate t ranges by determining its t dependence may bring about a confrontation of the experimental results in these complementary regimes. The Tevatron and HERA results pertaining to hard diffractive scattering cannot be directly compared at the moment, due to a lack of understanding of the gap survival probabilities. One possible route to achieve a more stringent comparison of the Tevatron and HERA data may be for the Tevatron experiments to try to measure the diffractive contribution to their data in a regime where the survival probability is expected to be high, i.e., for a sample with very high x_p. (The HERA experiments cannot do the converse and go to very low x_g while remaining in the regime of applicability of perturbative QCD.) The Tevatron constraint on the S_IP - c_g plane from measurements of diffractive hard scattering is only barely consistent with the HERA constraint at present. (They find, for instance, that S_IP must be less than 0.5 if c_g ~ 0.5 [23].) We look forward to an exciting comparison in the near future. As for the confrontation between experiment and theory, neither are presently precise enough for any strong statements to be made and much work remains to be done.

5. Acknowledgements

It is a pleasure to acknowledge assistance from Tony Doyle, Claudia Glasman, Dino Goulianos and Brent May.

References

[1]: ZEUS Collab., M. Derrick et al., Phys. Lett. B369 (1996) 55.
[2]: ZEUS Collab., M. Derrick et al., Phys. Lett. B356 (1995) 129.
[3]: ZEUS Collab., M. Derrick et al., Phys. Lett. B348 (1995) 665.
[4]: J. D. Bjorken, in International Workshop on Deep Inelastic Scattering and Related Subjects, Eilat, Israel, ed. A. Levy (World Scientific, 1994) 151.
[5]: A. H. Mueller and W.-K. Tang, Phys. Lett. B284 (1992) 123.
[6]: V. Del Duca and W.-K. Tang, Phys. Lett. B312 (1993) 225.
[7]: J. Pumplin, Phys. Rev. D50 (1994) 6811.
[8]: H.-U. Bengtsson and T. Sjöstrand, Comp. Phys. Comm. 46 (1987) 43.
[9]: T. Sjöstrand, CERN-TH.6488/92 (1992).
[10]: H1 Collab., I. Abt et al., Nucl. Phys. B445 (1995) 195.
[11]: ZEUS Collab., M. Derrick et al., in Proceedings of the International Europhysics Conference on HEP, Brussels (1995) EPS-0380.
[12]: L. E. Sinclair, Ph.D. thesis, McGill University (1996).
[13]: J. D. Bjorken, Phys. Rev. D47 (1992) 101.
[14]: E. Gotsman et al., Phys. Lett. B309 (1993) 199.
[15]: R. S. Fletcher and T. Stelzer, Phys. Rev. D48 (1993) 5162.
[16]: D0 Collab., S. Abachi et al., Phys. Rev. Lett. 76 (1996) 734.
[17]: CDF Collab., F. Abe et al., Phys. Rev. Lett. 74 (1995) 885.
[18]: P. Bruni and G. Ingelman, in Proceedings of the International Europhysics Conference, Marseille, France, July 1993, eds. J. Carr and M. Perrotet, (Ed. Frontieres, Gif-sur-Yvette, 1994) 595.
[19]: G. Ingelman and P. E. Sclein, Phys. Lett. B152 (1985) 256.
[20]: ZEUS Collab., M. Derrick et al., Phys. Lett. B342 (1995) 417.
[21]: H1 Collab., I. Abt et al., Phys. Lett. B348 (1995) 681.
[22]: ZEUS Collab., M. Derrick et al., Z. Phys. C68 (1995) 29.
[23]: K. Goulianos, in Topical Conference on Hard Diffractive Processes, Eilat, Israel (February, 1996).

Footnotes:

¹ e-mail: sinclair@desy.de

² For instance, a typical event with two jets of E_T^jet = 6 GeV at Dh = 3 at HERA would have x_g = 0.8while the corresponding event at the Tevatron with two jets of E_T^jet = 30 GeV and Dh = 3 would have x_p = 0.09.

File translated from T_EX by T_TH, version 0.9.