NOTES ON BQI 8/4/2024
------------
------------
These notes give a brief description of Burst Quality Indicators
that, as the name implies, are intended to describe the quality
of bursts. Below the BQI are identified in capitals.
The general characteristics of a burst are introduced and the parameters used
to describe these characteristics are illustrated below by run 13320, burst 1211;
this burst appears to be typical of a substantial fraction of the
NA62 data.
1) The spill distribution.
--------------------------
Fig 1 shows a set of figures that illustrate the general burst characteristics.
Fig. 1.0 spill trigger time vs trigger time modulo the SPS period
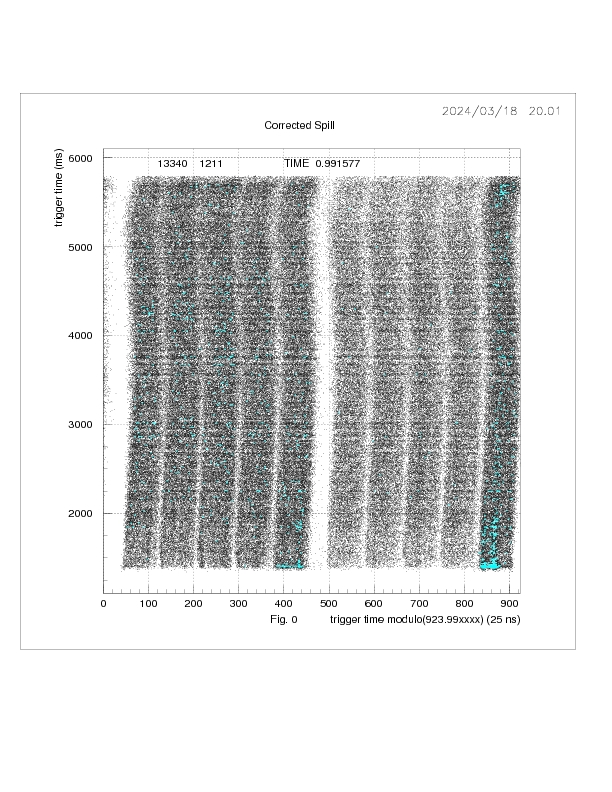 Fig 1.0 shows the spill in 2D. The X axis is the trigger time modulo the SPS period
(the folded spill time) with a cubic correction to partially linearize the distribution
in folded spill time. The Y axis is the trigger time.
This plot is also used used to determine the SPS period (see TIME + 923 at the top of Fig. 0 in
25 ns units).
Evidently the spill is not debunched and there is substantial low and high frequency noise
modulating the spill. The high intensity regions of the spill are indicated in cyan.
Figs 1.4 - 1.7 Spill distributions and low-frequency Fourier Analysis.
Fig 1.0 shows the spill in 2D. The X axis is the trigger time modulo the SPS period
(the folded spill time) with a cubic correction to partially linearize the distribution
in folded spill time. The Y axis is the trigger time.
This plot is also used used to determine the SPS period (see TIME + 923 at the top of Fig. 0 in
25 ns units).
Evidently the spill is not debunched and there is substantial low and high frequency noise
modulating the spill. The high intensity regions of the spill are indicated in cyan.
Figs 1.4 - 1.7 Spill distributions and low-frequency Fourier Analysis.
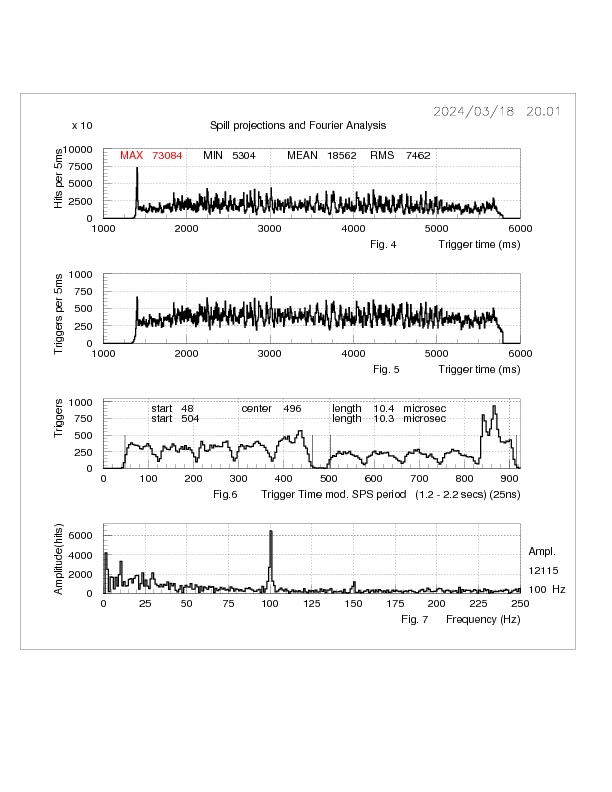 Fig 1.4 shows the number of GTK1 hits per trigger in 5ms bins of trigger time.
(An alternative would be number of triggers in 5ms of trigger time
but this shows a reduced variablity due to trigger dead-time, see Fig. 1.5).
The distribution is characterised by the MEAN , RMS(SD), MAX/MIN
of the spill. The MEAN, RMS and MIN are determined from the 2-5 sec region
of the spill.
The spill is characterised by an RMS considerably greater than the sqrt(MEAN) expected from
Poisson statistics. Frequently there is a sharp 'spike' of high intensity
at the start of the spill that is evident in the number of hits in GTK1.
The 'noise' in the spill is measured by a Fourier analysis (Fig 1.7).
This Figure shows that there is a substantial level of low frequency noise,
together with resonances at 50, 100, and 150 Hz.
The BQIs have been chosen to
be the amplitudes of the LOW , 50 and 100 Hz signals since these are frequently
the main contributors to the high RMS of the spill ( and GTK hit distribution).
High frequency noise is also present as shown in the folded
spill distributionis of Figs 1.0 , 1.2, 1.6 . These large high-frequency
variations of intensity are correlated with the sps period and are discussed
in more detail in the next Section.
2) GTK measurements of Bursts
-----------------------------
In general, the characteristics of a burst will be measured
in terms of the number of hits in GTK1. GTK hits are used rather than tiggers
since they are less influenced by dead time.
The number of hits in GTK1 are taken to be a measure of the beam intensity.
Figs 1.1 - Figs. 1.3 GTK1 hits per trigger, hits per trigger mod sps-period
Fig 1.4 shows the number of GTK1 hits per trigger in 5ms bins of trigger time.
(An alternative would be number of triggers in 5ms of trigger time
but this shows a reduced variablity due to trigger dead-time, see Fig. 1.5).
The distribution is characterised by the MEAN , RMS(SD), MAX/MIN
of the spill. The MEAN, RMS and MIN are determined from the 2-5 sec region
of the spill.
The spill is characterised by an RMS considerably greater than the sqrt(MEAN) expected from
Poisson statistics. Frequently there is a sharp 'spike' of high intensity
at the start of the spill that is evident in the number of hits in GTK1.
The 'noise' in the spill is measured by a Fourier analysis (Fig 1.7).
This Figure shows that there is a substantial level of low frequency noise,
together with resonances at 50, 100, and 150 Hz.
The BQIs have been chosen to
be the amplitudes of the LOW , 50 and 100 Hz signals since these are frequently
the main contributors to the high RMS of the spill ( and GTK hit distribution).
High frequency noise is also present as shown in the folded
spill distributionis of Figs 1.0 , 1.2, 1.6 . These large high-frequency
variations of intensity are correlated with the sps period and are discussed
in more detail in the next Section.
2) GTK measurements of Bursts
-----------------------------
In general, the characteristics of a burst will be measured
in terms of the number of hits in GTK1. GTK hits are used rather than tiggers
since they are less influenced by dead time.
The number of hits in GTK1 are taken to be a measure of the beam intensity.
Figs 1.1 - Figs. 1.3 GTK1 hits per trigger, hits per trigger mod sps-period
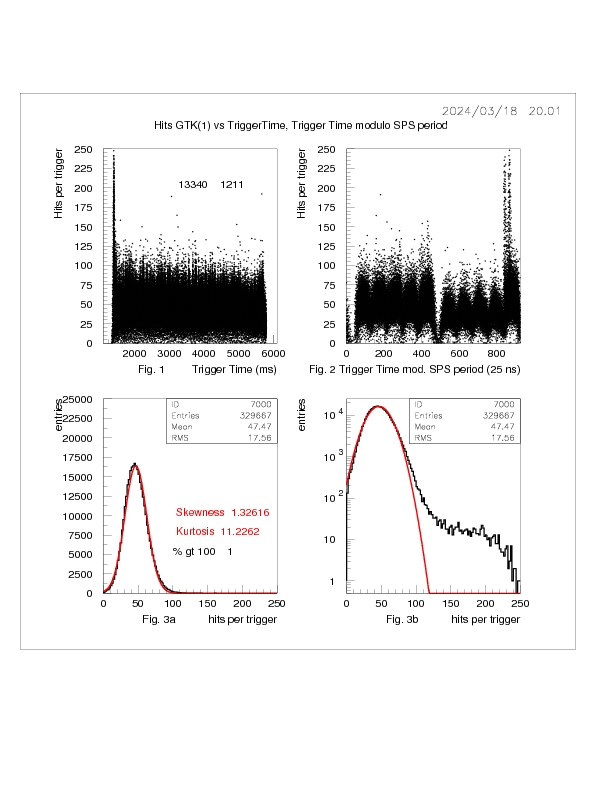 Figs 1.1 and 1.2 are scatterplots of GTK1 hits per trigger versus
trigger time and hits versus trigger time modulo the SPS period, respectively.
This burst is characterised by a high intensity spike at the start of the
spill that fig 1.2 shows is a double spike in the tenth bunch (see also Fig. 1.5).
There is also a reduction in intensity in bunches 5-10 relative to 1-5.
No attempt has been made to parametrise this structure since it is
dependent on an accurate determination of the SPS period for the run
- a cpu intensive operation.
The distribution of the number of hits per trigger in GTK 1 (Fig 1.3a,1.3b)
is, to a good approximation, Gaussian in shape (Fig. 1.3a),
but a tail is present in many cases as shown by the
log plot (Fig. 1.3b).
The Gaussian distribution is described by the MEAN and STANDARD DEVIATION(SD or RMS).
These are ~ 50 hits/trigger and ~15 hits/trigger, respectively.
Notice that the RMS is about a factor 2 larger than expected from the
value of the mean. This is due to the lack uf uniformity of
the spill (see Fig 1.0 , Fig 1.4, Fig. 1.5 ) and is further discussed below in relation
to the spill duty factor.
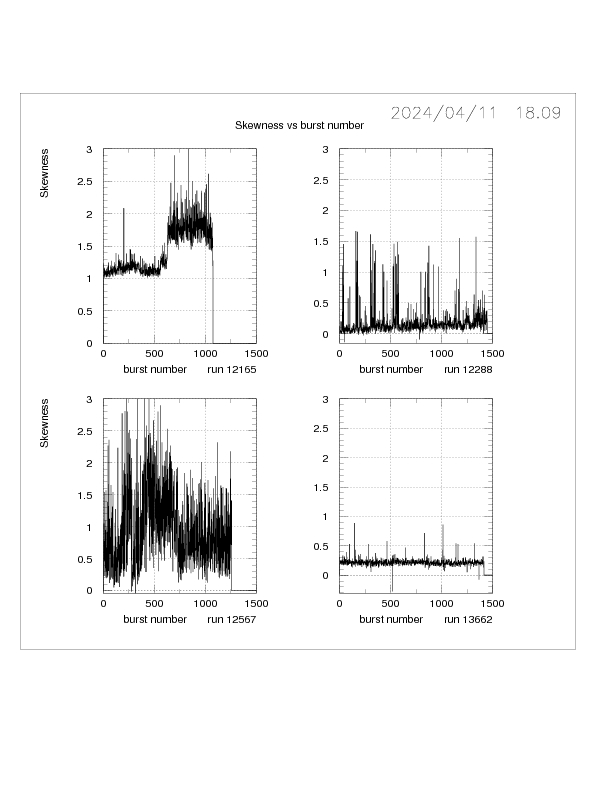
The deviation of the hit distribution from a gaussian distribution
is measured by the SKEWNESS and KURTOSIS parameters.
SKEWNESS = (3rd moment of distribution)/SD**3 0. for Gaussian
KURTOSIS = (4th moment)/SD*4 3. for Gaussian
Skewness measures the asymmetry of the distribution, whereas
kurtosis measures the the tails of the distribution:
leptokurtic = long tails , platykurtic = more peaked than Gaussian.
SKEWNESS and KURTOSIS are highly correlated for these data.
The skewness is of particular importance since it turns out to be
a good indicator of a high intensity component of the spill.
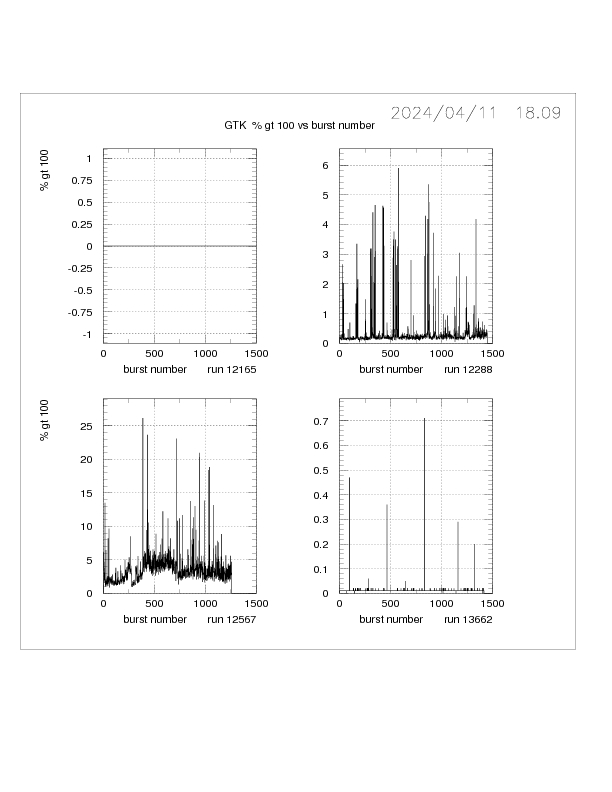
Another parameter that is used to describe the GTK hit distribution
is the % HITS GREATER THAN 100.
This gives an alternative measure of the tail of the distribution and is
strongly correlated with the skewness and RMS. There is also a weaker correlation
with the RMS and MEAN. The 100 counts limit is chosen since the hit distribution
is close to normal below this count.
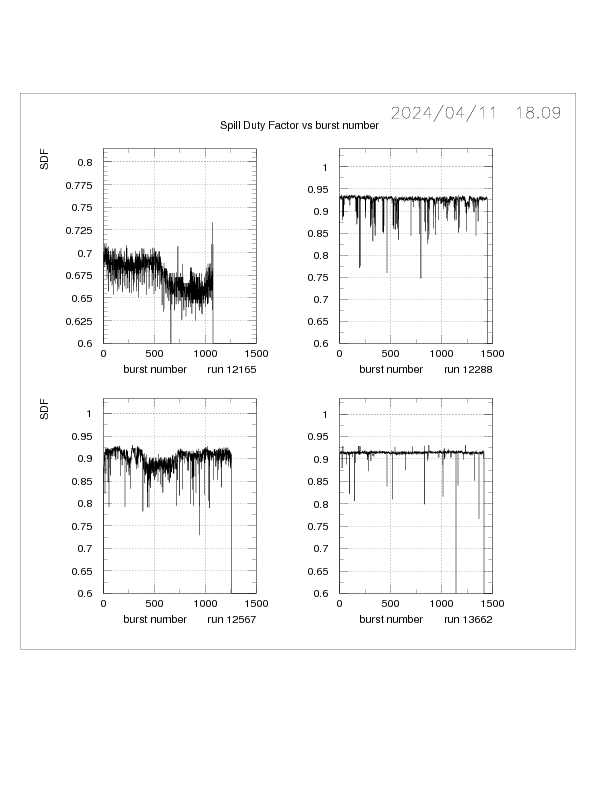
3)Spill Duty Factor and normalised RMS
--------------------------------------
The Spill Duty Factor (SDF) is used to parameterise the uniformity of a particle beam.
This is defined as
(mean intensity)**2/(mean of intensity**2).
Thus a uniform beam would have a SDF of unity and any variations in
in intensty would reduce the SDF.
In the absence of the availability of a direct measure of the beam intensity
the SDF is calculated from MEAN**2/(MEAN**2 + RMS**2) from GTK1.
See Figs. 2 and 3
for plots of the SDF for low (12288) and higher (12567) beam intensity
runs, respectively.
Fig. 2 SDF for run 12288
Figs 1.1 and 1.2 are scatterplots of GTK1 hits per trigger versus
trigger time and hits versus trigger time modulo the SPS period, respectively.
This burst is characterised by a high intensity spike at the start of the
spill that fig 1.2 shows is a double spike in the tenth bunch (see also Fig. 1.5).
There is also a reduction in intensity in bunches 5-10 relative to 1-5.
No attempt has been made to parametrise this structure since it is
dependent on an accurate determination of the SPS period for the run
- a cpu intensive operation.
The distribution of the number of hits per trigger in GTK 1 (Fig 1.3a,1.3b)
is, to a good approximation, Gaussian in shape (Fig. 1.3a),
but a tail is present in many cases as shown by the
log plot (Fig. 1.3b).
The Gaussian distribution is described by the MEAN and STANDARD DEVIATION(SD or RMS).
These are ~ 50 hits/trigger and ~15 hits/trigger, respectively.
Notice that the RMS is about a factor 2 larger than expected from the
value of the mean. This is due to the lack uf uniformity of
the spill (see Fig 1.0 , Fig 1.4, Fig. 1.5 ) and is further discussed below in relation
to the spill duty factor.
The deviation of the hit distribution from a gaussian distribution
is measured by the SKEWNESS and KURTOSIS parameters.
SKEWNESS = (3rd moment of distribution)/SD**3 0. for Gaussian
KURTOSIS = (4th moment)/SD*4 3. for Gaussian
Skewness measures the asymmetry of the distribution, whereas
kurtosis measures the the tails of the distribution:
leptokurtic = long tails , platykurtic = more peaked than Gaussian.
SKEWNESS and KURTOSIS are highly correlated for these data.
The skewness is of particular importance since it turns out to be
a good indicator of a high intensity component of the spill.
Another parameter that is used to describe the GTK hit distribution
is the % HITS GREATER THAN 100.
This gives an alternative measure of the tail of the distribution and is
strongly correlated with the skewness and RMS. There is also a weaker correlation
with the RMS and MEAN. The 100 counts limit is chosen since the hit distribution
is close to normal below this count.
3)Spill Duty Factor and normalised RMS
--------------------------------------
The Spill Duty Factor (SDF) is used to parameterise the uniformity of a particle beam.
This is defined as
(mean intensity)**2/(mean of intensity**2).
Thus a uniform beam would have a SDF of unity and any variations in
in intensty would reduce the SDF.
In the absence of the availability of a direct measure of the beam intensity
the SDF is calculated from MEAN**2/(MEAN**2 + RMS**2) from GTK1.
See Figs. 2 and 3
for plots of the SDF for low (12288) and higher (12567) beam intensity
runs, respectively.
Fig. 2 SDF for run 12288
 Fig. 3 SDF for run 12567
Fig. 3 SDF for run 12567
 For run 12288 with statistical noise only, the SDF would be expected to
be ~0.98 . A value of ~0.92 is found due to the RMS of the beam
as measured by GTK1 being a factor ~2 larger than that expected
for a Poisson distribution. In addition, some bursts have lower
values of the SDF due to the 100 Hz oscillation ( see Figs 4,5).
The higher intensity run 12567 has a lower mean SDF togther with a larger
statistical fluctuations due to general noise in the spill.
The yellow bands in Figs 2 and 3 indicate the range expected for the SDF
for a mean between 40 and 60 hits per trigger in the GTK with
an RMS ~ 2*sqrt(mean).
An alternative to the SDF is a normalised RMS . If the noise in the spill
were due only to Poissonian fluctuations the RMS of the spill would have
an RMS equal to sqrt of the mean of the spill. Consequently the value of
RMS/sqrt(MEAN) would be equal to unity.
A study of 2024 data indicates that a value greater than three for the
normalised RMS indicates a low quality burst at the 2 sd level.
4) Correlations between BQIs
----------------------------
Fig 4 Run 12288 RMS GTK1 and Fourier amplitudes
For run 12288 with statistical noise only, the SDF would be expected to
be ~0.98 . A value of ~0.92 is found due to the RMS of the beam
as measured by GTK1 being a factor ~2 larger than that expected
for a Poisson distribution. In addition, some bursts have lower
values of the SDF due to the 100 Hz oscillation ( see Figs 4,5).
The higher intensity run 12567 has a lower mean SDF togther with a larger
statistical fluctuations due to general noise in the spill.
The yellow bands in Figs 2 and 3 indicate the range expected for the SDF
for a mean between 40 and 60 hits per trigger in the GTK with
an RMS ~ 2*sqrt(mean).
An alternative to the SDF is a normalised RMS . If the noise in the spill
were due only to Poissonian fluctuations the RMS of the spill would have
an RMS equal to sqrt of the mean of the spill. Consequently the value of
RMS/sqrt(MEAN) would be equal to unity.
A study of 2024 data indicates that a value greater than three for the
normalised RMS indicates a low quality burst at the 2 sd level.
4) Correlations between BQIs
----------------------------
Fig 4 Run 12288 RMS GTK1 and Fourier amplitudes
 Fig 5 Run 12288 Triggers/burst,Mean, RMS, Skewness, SDF
Fig 5 Run 12288 Triggers/burst,Mean, RMS, Skewness, SDF
 Figs. 4 and 5 show the correlations between the bunch parameters for run 12288.
Evidently, there can be strong correlations between the skewness, the Fourier
analysis and RMS that are reflected in the SDF.
5)General Run Characteristics
------------------------------
Fig. 6 Spill-maximum and Trigger-time of spill-maximum.
(To be replaced by GTK hits/trigger)
Figs. 4 and 5 show the correlations between the bunch parameters for run 12288.
Evidently, there can be strong correlations between the skewness, the Fourier
analysis and RMS that are reflected in the SDF.
5)General Run Characteristics
------------------------------
Fig. 6 Spill-maximum and Trigger-time of spill-maximum.
(To be replaced by GTK hits/trigger)
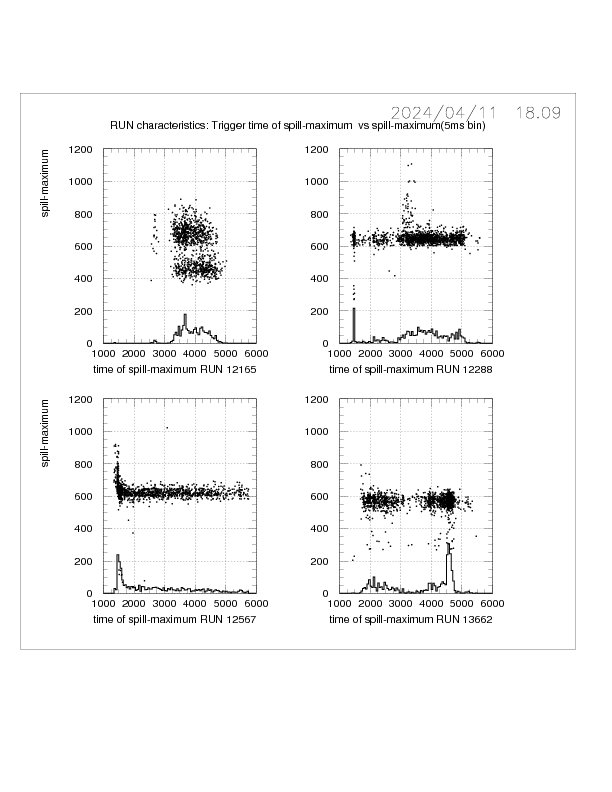 The lack of uniformity of the spill suggests that the time of the maximum
of the spill, and its value, could be a useful parameterisation of a run.
Plots of the time of the spill-maximum vs spill maximum are shown in Fig. 6
for four runs. The spill maximum/time is determined here from a plot of trigger time in 5 ms bins.
In the scatterplots each point repesents a bust; the histogram is a projection of the scatterplot on the
time-maximum axis. A uniforn spill would be dispayed as a uniform band of points in the scatterplot.
These four runs illustrate the various departures from uniformity that can occur: namely intensity peaks
at the start and end of the spill and changes in maximum intensity along the spill.
Fig. 7 GTK1 RMS per burst
The lack of uniformity of the spill suggests that the time of the maximum
of the spill, and its value, could be a useful parameterisation of a run.
Plots of the time of the spill-maximum vs spill maximum are shown in Fig. 6
for four runs. The spill maximum/time is determined here from a plot of trigger time in 5 ms bins.
In the scatterplots each point repesents a bust; the histogram is a projection of the scatterplot on the
time-maximum axis. A uniforn spill would be dispayed as a uniform band of points in the scatterplot.
These four runs illustrate the various departures from uniformity that can occur: namely intensity peaks
at the start and end of the spill and changes in maximum intensity along the spill.
Fig. 7 GTK1 RMS per burst
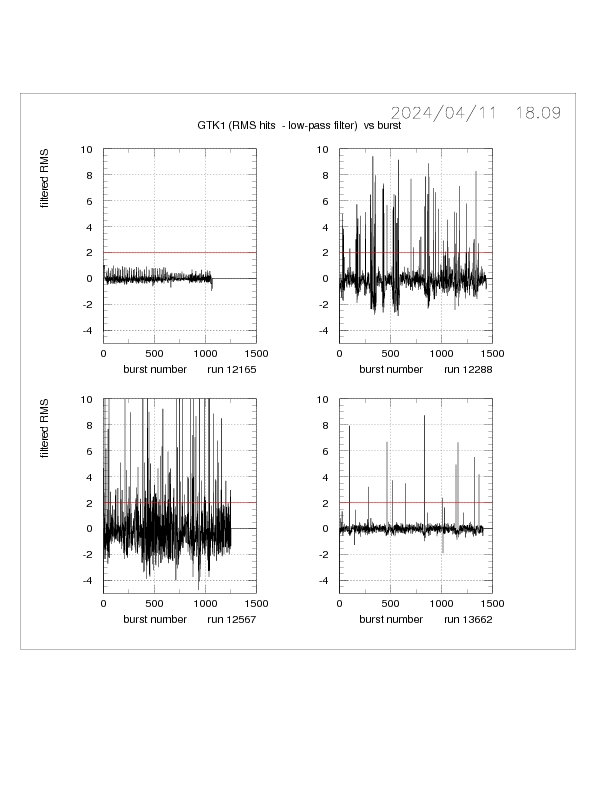 Another parameter illustating the overall characteristics of a run is the
RMS of the GTK 1 hits per trigger calculated per burst (see Section 2 Fig. 3a ).
This is shown in Fig. 7 for four runs. Here a high-pass filtered RMS is plotted
against burst number.
High RMS bursts are evident in three runs. A detailed study shows that the high-RMS
bursts are primarily due to 100 Hz and 50 Hz noise for runs 12288 and 13362, respectively.
6) Summary and conclusions.
-----------------------
Bursts with a high intensity component have a high RMS, low SDF and
high skewness of the GTK1 distribution and are identifiable using these and other BQIs.
Since the NA62 trigger is paralyzable there is little dependence of the
number of pnunu events on beam intensity. In contrast, the upstream
background and pileup are at least proportional to the beam intensity.
Consequently, if it is desired to minimimise the background in the event selection,
the BQI introduced here would provide the opportunity to do so.
Addendum 1
--------
Additional BQI plots for SDF, skewness, % greater than 100, mean and RMS for GTK1
Another parameter illustating the overall characteristics of a run is the
RMS of the GTK 1 hits per trigger calculated per burst (see Section 2 Fig. 3a ).
This is shown in Fig. 7 for four runs. Here a high-pass filtered RMS is plotted
against burst number.
High RMS bursts are evident in three runs. A detailed study shows that the high-RMS
bursts are primarily due to 100 Hz and 50 Hz noise for runs 12288 and 13362, respectively.
6) Summary and conclusions.
-----------------------
Bursts with a high intensity component have a high RMS, low SDF and
high skewness of the GTK1 distribution and are identifiable using these and other BQIs.
Since the NA62 trigger is paralyzable there is little dependence of the
number of pnunu events on beam intensity. In contrast, the upstream
background and pileup are at least proportional to the beam intensity.
Consequently, if it is desired to minimimise the background in the event selection,
the BQI introduced here would provide the opportunity to do so.
Addendum 1
--------
Additional BQI plots for SDF, skewness, % greater than 100, mean and RMS for GTK1
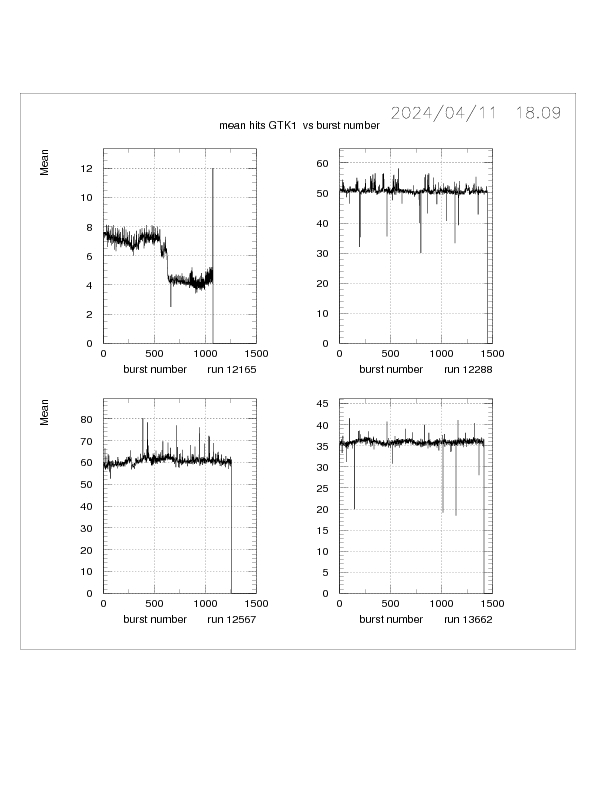
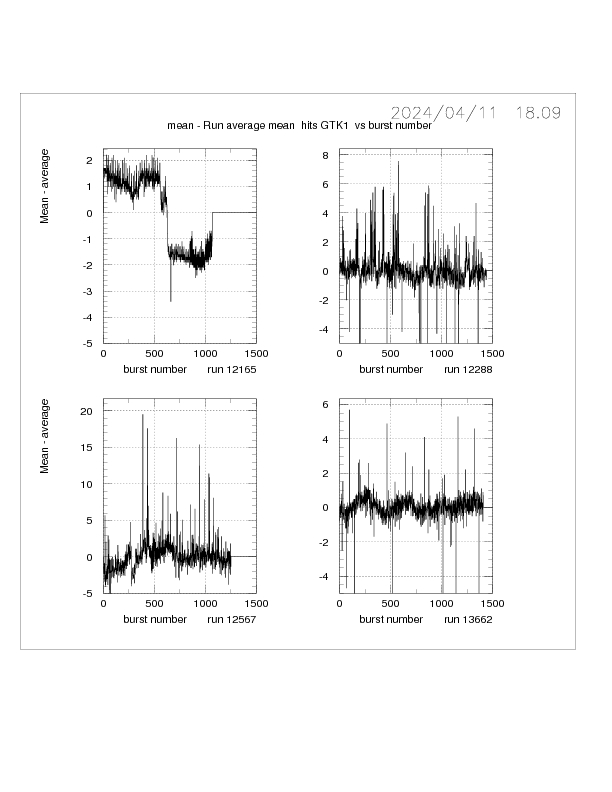
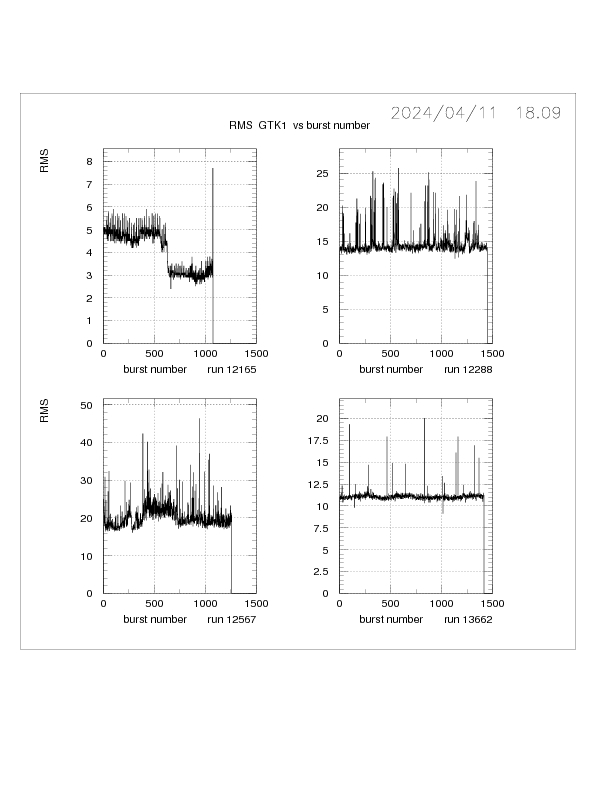
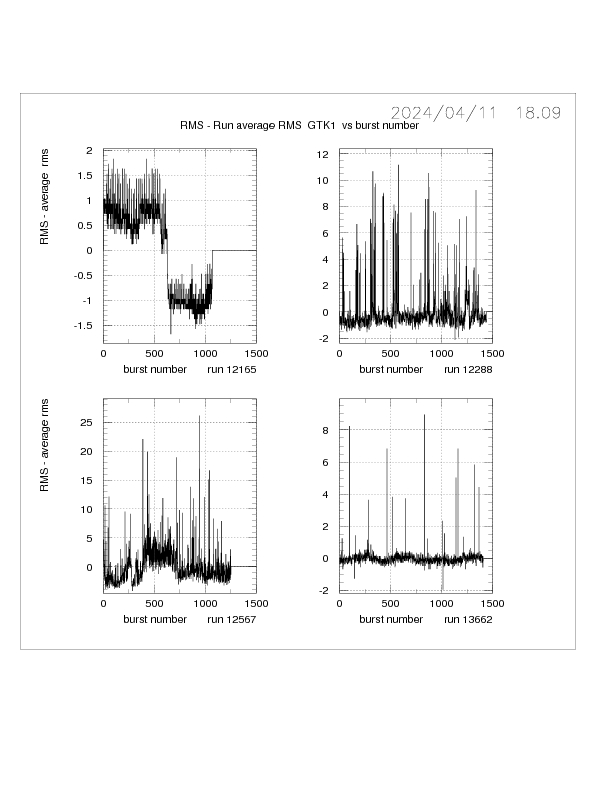 Addemdum 2
---------
Plots for max vs spill time of max.
Plots for mean, rms.
Addemdum 2
---------
Plots for max vs spill time of max.
Plots for mean, rms.
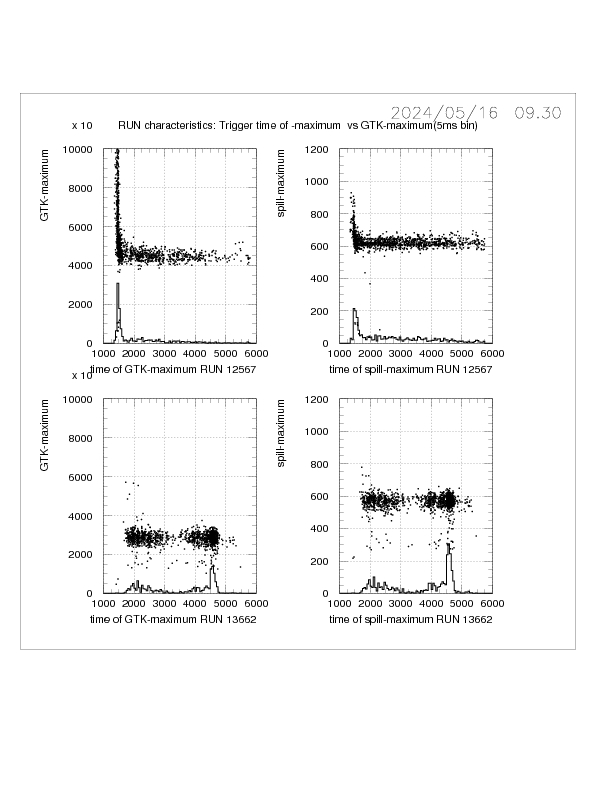
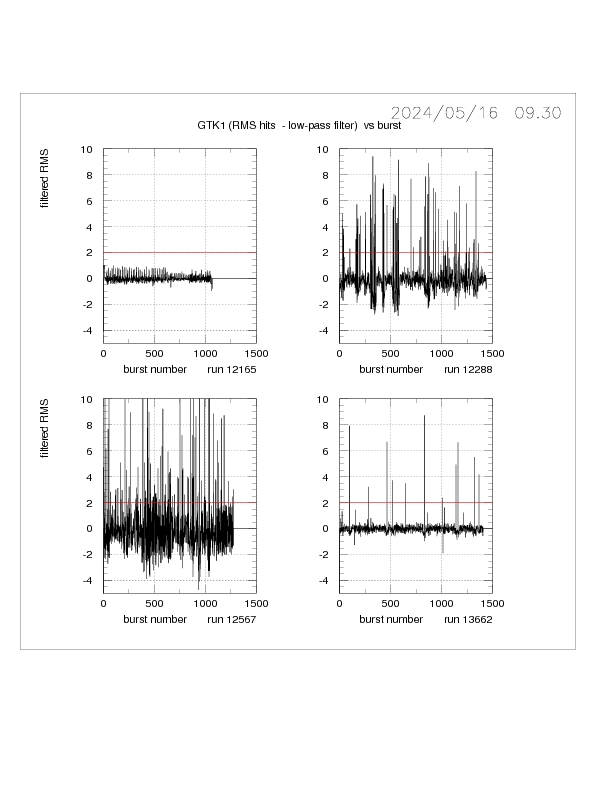
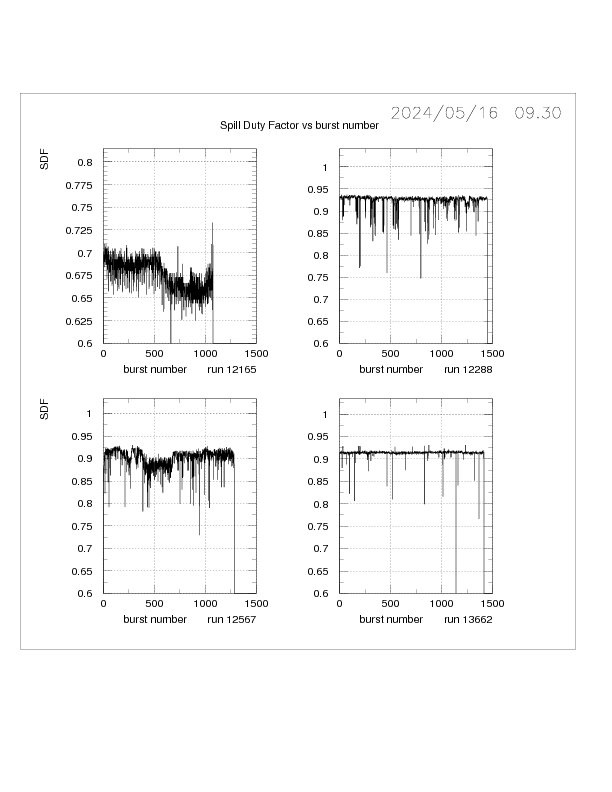
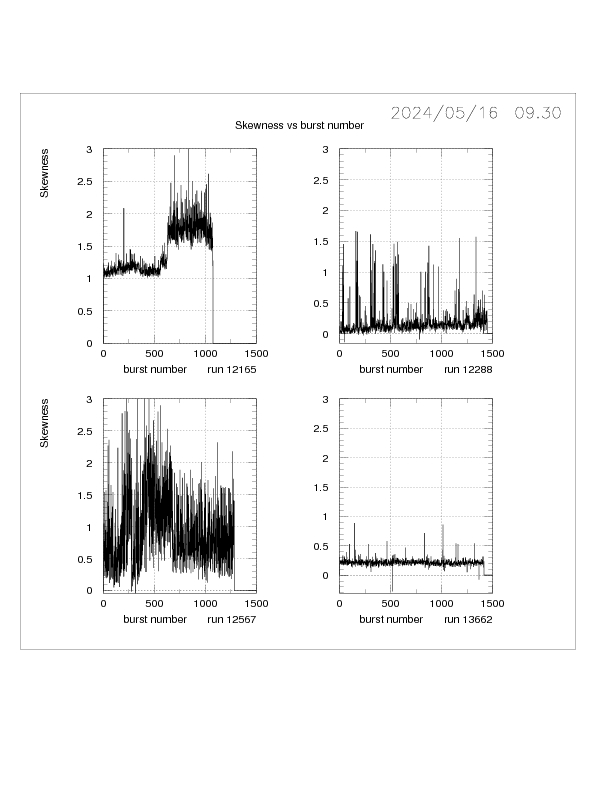
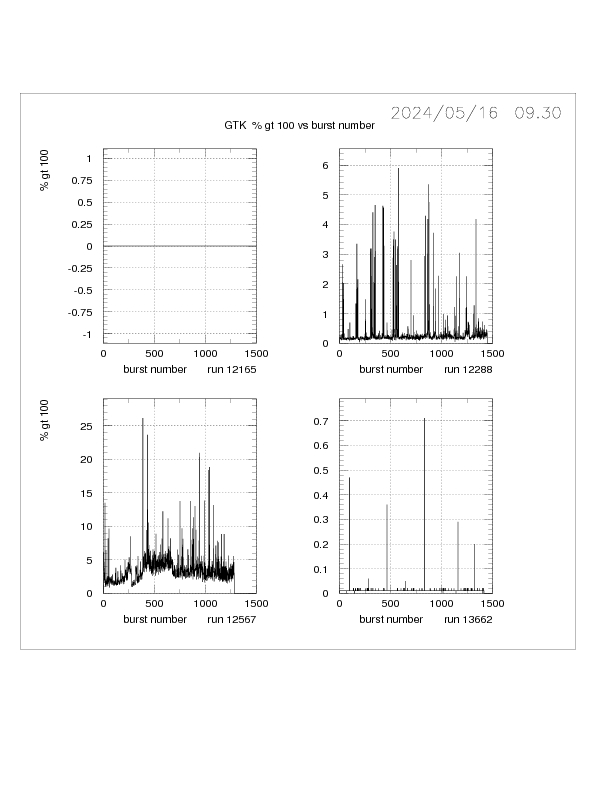
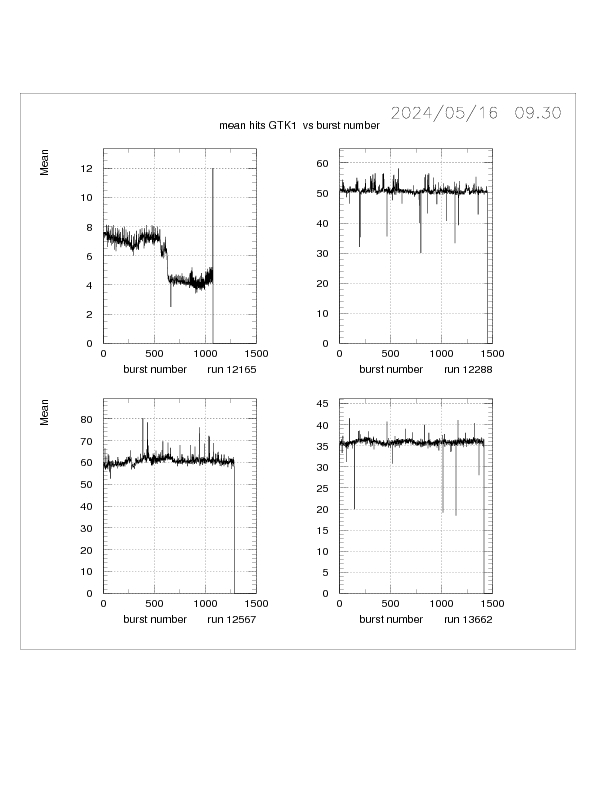
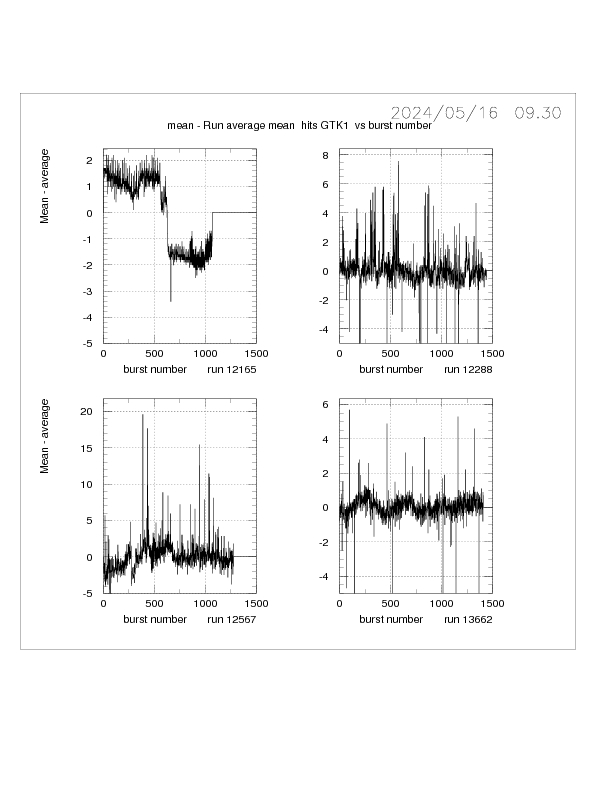
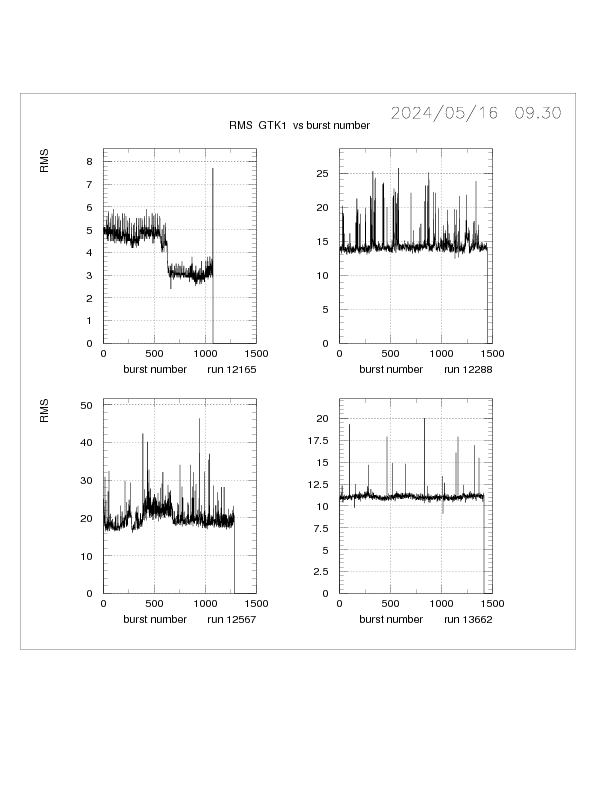
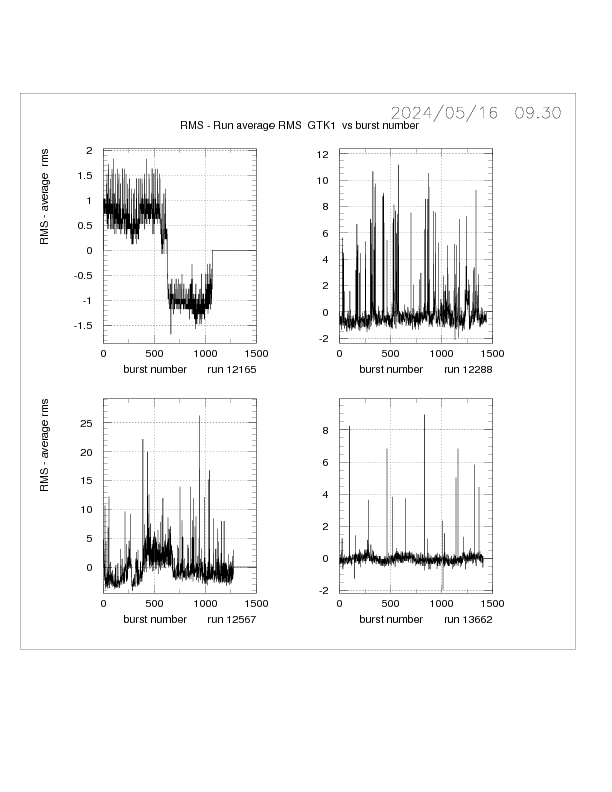
 Fig 1.0 shows the spill in 2D. The X axis is the trigger time modulo the SPS period
(the folded spill time) with a cubic correction to partially linearize the distribution
in folded spill time. The Y axis is the trigger time.
This plot is also used used to determine the SPS period (see TIME + 923 at the top of Fig. 0 in
25 ns units).
Evidently the spill is not debunched and there is substantial low and high frequency noise
modulating the spill. The high intensity regions of the spill are indicated in cyan.
Figs 1.4 - 1.7 Spill distributions and low-frequency Fourier Analysis.
Fig 1.0 shows the spill in 2D. The X axis is the trigger time modulo the SPS period
(the folded spill time) with a cubic correction to partially linearize the distribution
in folded spill time. The Y axis is the trigger time.
This plot is also used used to determine the SPS period (see TIME + 923 at the top of Fig. 0 in
25 ns units).
Evidently the spill is not debunched and there is substantial low and high frequency noise
modulating the spill. The high intensity regions of the spill are indicated in cyan.
Figs 1.4 - 1.7 Spill distributions and low-frequency Fourier Analysis.
 Fig 1.4 shows the number of GTK1 hits per trigger in 5ms bins of trigger time.
(An alternative would be number of triggers in 5ms of trigger time
but this shows a reduced variablity due to trigger dead-time, see Fig. 1.5).
The distribution is characterised by the MEAN , RMS(SD), MAX/MIN
of the spill. The MEAN, RMS and MIN are determined from the 2-5 sec region
of the spill.
The spill is characterised by an RMS considerably greater than the sqrt(MEAN) expected from
Poisson statistics. Frequently there is a sharp 'spike' of high intensity
at the start of the spill that is evident in the number of hits in GTK1.
The 'noise' in the spill is measured by a Fourier analysis (Fig 1.7).
This Figure shows that there is a substantial level of low frequency noise,
together with resonances at 50, 100, and 150 Hz.
The BQIs have been chosen to
be the amplitudes of the LOW , 50 and 100 Hz signals since these are frequently
the main contributors to the high RMS of the spill ( and GTK hit distribution).
High frequency noise is also present as shown in the folded
spill distributionis of Figs 1.0 , 1.2, 1.6 . These large high-frequency
variations of intensity are correlated with the sps period and are discussed
in more detail in the next Section.
2) GTK measurements of Bursts
-----------------------------
In general, the characteristics of a burst will be measured
in terms of the number of hits in GTK1. GTK hits are used rather than tiggers
since they are less influenced by dead time.
The number of hits in GTK1 are taken to be a measure of the beam intensity.
Figs 1.1 - Figs. 1.3 GTK1 hits per trigger, hits per trigger mod sps-period
Fig 1.4 shows the number of GTK1 hits per trigger in 5ms bins of trigger time.
(An alternative would be number of triggers in 5ms of trigger time
but this shows a reduced variablity due to trigger dead-time, see Fig. 1.5).
The distribution is characterised by the MEAN , RMS(SD), MAX/MIN
of the spill. The MEAN, RMS and MIN are determined from the 2-5 sec region
of the spill.
The spill is characterised by an RMS considerably greater than the sqrt(MEAN) expected from
Poisson statistics. Frequently there is a sharp 'spike' of high intensity
at the start of the spill that is evident in the number of hits in GTK1.
The 'noise' in the spill is measured by a Fourier analysis (Fig 1.7).
This Figure shows that there is a substantial level of low frequency noise,
together with resonances at 50, 100, and 150 Hz.
The BQIs have been chosen to
be the amplitudes of the LOW , 50 and 100 Hz signals since these are frequently
the main contributors to the high RMS of the spill ( and GTK hit distribution).
High frequency noise is also present as shown in the folded
spill distributionis of Figs 1.0 , 1.2, 1.6 . These large high-frequency
variations of intensity are correlated with the sps period and are discussed
in more detail in the next Section.
2) GTK measurements of Bursts
-----------------------------
In general, the characteristics of a burst will be measured
in terms of the number of hits in GTK1. GTK hits are used rather than tiggers
since they are less influenced by dead time.
The number of hits in GTK1 are taken to be a measure of the beam intensity.
Figs 1.1 - Figs. 1.3 GTK1 hits per trigger, hits per trigger mod sps-period
 Figs 1.1 and 1.2 are scatterplots of GTK1 hits per trigger versus
trigger time and hits versus trigger time modulo the SPS period, respectively.
This burst is characterised by a high intensity spike at the start of the
spill that fig 1.2 shows is a double spike in the tenth bunch (see also Fig. 1.5).
There is also a reduction in intensity in bunches 5-10 relative to 1-5.
No attempt has been made to parametrise this structure since it is
dependent on an accurate determination of the SPS period for the run
- a cpu intensive operation.
The distribution of the number of hits per trigger in GTK 1 (Fig 1.3a,1.3b)
is, to a good approximation, Gaussian in shape (Fig. 1.3a),
but a tail is present in many cases as shown by the
log plot (Fig. 1.3b).
The Gaussian distribution is described by the MEAN and STANDARD DEVIATION(SD or RMS).
These are ~ 50 hits/trigger and ~15 hits/trigger, respectively.
Notice that the RMS is about a factor 2 larger than expected from the
value of the mean. This is due to the lack uf uniformity of
the spill (see Fig 1.0 , Fig 1.4, Fig. 1.5 ) and is further discussed below in relation
to the spill duty factor.
The deviation of the hit distribution from a gaussian distribution
is measured by the SKEWNESS and KURTOSIS parameters.
SKEWNESS = (3rd moment of distribution)/SD**3 0. for Gaussian
KURTOSIS = (4th moment)/SD*4 3. for Gaussian
Skewness measures the asymmetry of the distribution, whereas
kurtosis measures the the tails of the distribution:
leptokurtic = long tails , platykurtic = more peaked than Gaussian.
SKEWNESS and KURTOSIS are highly correlated for these data.
The skewness is of particular importance since it turns out to be
a good indicator of a high intensity component of the spill.
Another parameter that is used to describe the GTK hit distribution
is the % HITS GREATER THAN 100.
This gives an alternative measure of the tail of the distribution and is
strongly correlated with the skewness and RMS. There is also a weaker correlation
with the RMS and MEAN. The 100 counts limit is chosen since the hit distribution
is close to normal below this count.
3)Spill Duty Factor and normalised RMS
--------------------------------------
The Spill Duty Factor (SDF) is used to parameterise the uniformity of a particle beam.
This is defined as
(mean intensity)**2/(mean of intensity**2).
Thus a uniform beam would have a SDF of unity and any variations in
in intensty would reduce the SDF.
In the absence of the availability of a direct measure of the beam intensity
the SDF is calculated from MEAN**2/(MEAN**2 + RMS**2) from GTK1.
See Figs. 2 and 3
for plots of the SDF for low (12288) and higher (12567) beam intensity
runs, respectively.
Fig. 2 SDF for run 12288
Figs 1.1 and 1.2 are scatterplots of GTK1 hits per trigger versus
trigger time and hits versus trigger time modulo the SPS period, respectively.
This burst is characterised by a high intensity spike at the start of the
spill that fig 1.2 shows is a double spike in the tenth bunch (see also Fig. 1.5).
There is also a reduction in intensity in bunches 5-10 relative to 1-5.
No attempt has been made to parametrise this structure since it is
dependent on an accurate determination of the SPS period for the run
- a cpu intensive operation.
The distribution of the number of hits per trigger in GTK 1 (Fig 1.3a,1.3b)
is, to a good approximation, Gaussian in shape (Fig. 1.3a),
but a tail is present in many cases as shown by the
log plot (Fig. 1.3b).
The Gaussian distribution is described by the MEAN and STANDARD DEVIATION(SD or RMS).
These are ~ 50 hits/trigger and ~15 hits/trigger, respectively.
Notice that the RMS is about a factor 2 larger than expected from the
value of the mean. This is due to the lack uf uniformity of
the spill (see Fig 1.0 , Fig 1.4, Fig. 1.5 ) and is further discussed below in relation
to the spill duty factor.
The deviation of the hit distribution from a gaussian distribution
is measured by the SKEWNESS and KURTOSIS parameters.
SKEWNESS = (3rd moment of distribution)/SD**3 0. for Gaussian
KURTOSIS = (4th moment)/SD*4 3. for Gaussian
Skewness measures the asymmetry of the distribution, whereas
kurtosis measures the the tails of the distribution:
leptokurtic = long tails , platykurtic = more peaked than Gaussian.
SKEWNESS and KURTOSIS are highly correlated for these data.
The skewness is of particular importance since it turns out to be
a good indicator of a high intensity component of the spill.
Another parameter that is used to describe the GTK hit distribution
is the % HITS GREATER THAN 100.
This gives an alternative measure of the tail of the distribution and is
strongly correlated with the skewness and RMS. There is also a weaker correlation
with the RMS and MEAN. The 100 counts limit is chosen since the hit distribution
is close to normal below this count.
3)Spill Duty Factor and normalised RMS
--------------------------------------
The Spill Duty Factor (SDF) is used to parameterise the uniformity of a particle beam.
This is defined as
(mean intensity)**2/(mean of intensity**2).
Thus a uniform beam would have a SDF of unity and any variations in
in intensty would reduce the SDF.
In the absence of the availability of a direct measure of the beam intensity
the SDF is calculated from MEAN**2/(MEAN**2 + RMS**2) from GTK1.
See Figs. 2 and 3
for plots of the SDF for low (12288) and higher (12567) beam intensity
runs, respectively.
Fig. 2 SDF for run 12288
 Fig. 3 SDF for run 12567
Fig. 3 SDF for run 12567
 For run 12288 with statistical noise only, the SDF would be expected to
be ~0.98 . A value of ~0.92 is found due to the RMS of the beam
as measured by GTK1 being a factor ~2 larger than that expected
for a Poisson distribution. In addition, some bursts have lower
values of the SDF due to the 100 Hz oscillation ( see Figs 4,5).
The higher intensity run 12567 has a lower mean SDF togther with a larger
statistical fluctuations due to general noise in the spill.
The yellow bands in Figs 2 and 3 indicate the range expected for the SDF
for a mean between 40 and 60 hits per trigger in the GTK with
an RMS ~ 2*sqrt(mean).
An alternative to the SDF is a normalised RMS . If the noise in the spill
were due only to Poissonian fluctuations the RMS of the spill would have
an RMS equal to sqrt of the mean of the spill. Consequently the value of
RMS/sqrt(MEAN) would be equal to unity.
A study of 2024 data indicates that a value greater than three for the
normalised RMS indicates a low quality burst at the 2 sd level.
4) Correlations between BQIs
----------------------------
Fig 4 Run 12288 RMS GTK1 and Fourier amplitudes
For run 12288 with statistical noise only, the SDF would be expected to
be ~0.98 . A value of ~0.92 is found due to the RMS of the beam
as measured by GTK1 being a factor ~2 larger than that expected
for a Poisson distribution. In addition, some bursts have lower
values of the SDF due to the 100 Hz oscillation ( see Figs 4,5).
The higher intensity run 12567 has a lower mean SDF togther with a larger
statistical fluctuations due to general noise in the spill.
The yellow bands in Figs 2 and 3 indicate the range expected for the SDF
for a mean between 40 and 60 hits per trigger in the GTK with
an RMS ~ 2*sqrt(mean).
An alternative to the SDF is a normalised RMS . If the noise in the spill
were due only to Poissonian fluctuations the RMS of the spill would have
an RMS equal to sqrt of the mean of the spill. Consequently the value of
RMS/sqrt(MEAN) would be equal to unity.
A study of 2024 data indicates that a value greater than three for the
normalised RMS indicates a low quality burst at the 2 sd level.
4) Correlations between BQIs
----------------------------
Fig 4 Run 12288 RMS GTK1 and Fourier amplitudes
 Fig 5 Run 12288 Triggers/burst,Mean, RMS, Skewness, SDF
Fig 5 Run 12288 Triggers/burst,Mean, RMS, Skewness, SDF
 Figs. 4 and 5 show the correlations between the bunch parameters for run 12288.
Evidently, there can be strong correlations between the skewness, the Fourier
analysis and RMS that are reflected in the SDF.
5)General Run Characteristics
------------------------------
Fig. 6 Spill-maximum and Trigger-time of spill-maximum.
(To be replaced by GTK hits/trigger)
Figs. 4 and 5 show the correlations between the bunch parameters for run 12288.
Evidently, there can be strong correlations between the skewness, the Fourier
analysis and RMS that are reflected in the SDF.
5)General Run Characteristics
------------------------------
Fig. 6 Spill-maximum and Trigger-time of spill-maximum.
(To be replaced by GTK hits/trigger)
 The lack of uniformity of the spill suggests that the time of the maximum
of the spill, and its value, could be a useful parameterisation of a run.
Plots of the time of the spill-maximum vs spill maximum are shown in Fig. 6
for four runs. The spill maximum/time is determined here from a plot of trigger time in 5 ms bins.
In the scatterplots each point repesents a bust; the histogram is a projection of the scatterplot on the
time-maximum axis. A uniforn spill would be dispayed as a uniform band of points in the scatterplot.
These four runs illustrate the various departures from uniformity that can occur: namely intensity peaks
at the start and end of the spill and changes in maximum intensity along the spill.
Fig. 7 GTK1 RMS per burst
The lack of uniformity of the spill suggests that the time of the maximum
of the spill, and its value, could be a useful parameterisation of a run.
Plots of the time of the spill-maximum vs spill maximum are shown in Fig. 6
for four runs. The spill maximum/time is determined here from a plot of trigger time in 5 ms bins.
In the scatterplots each point repesents a bust; the histogram is a projection of the scatterplot on the
time-maximum axis. A uniforn spill would be dispayed as a uniform band of points in the scatterplot.
These four runs illustrate the various departures from uniformity that can occur: namely intensity peaks
at the start and end of the spill and changes in maximum intensity along the spill.
Fig. 7 GTK1 RMS per burst
 Another parameter illustating the overall characteristics of a run is the
RMS of the GTK 1 hits per trigger calculated per burst (see Section 2 Fig. 3a ).
This is shown in Fig. 7 for four runs. Here a high-pass filtered RMS is plotted
against burst number.
High RMS bursts are evident in three runs. A detailed study shows that the high-RMS
bursts are primarily due to 100 Hz and 50 Hz noise for runs 12288 and 13362, respectively.
6) Summary and conclusions.
-----------------------
Bursts with a high intensity component have a high RMS, low SDF and
high skewness of the GTK1 distribution and are identifiable using these and other BQIs.
Since the NA62 trigger is paralyzable there is little dependence of the
number of pnunu events on beam intensity. In contrast, the upstream
background and pileup are at least proportional to the beam intensity.
Consequently, if it is desired to minimimise the background in the event selection,
the BQI introduced here would provide the opportunity to do so.
Addendum 1
--------
Additional BQI plots for SDF, skewness, % greater than 100, mean and RMS for GTK1
Another parameter illustating the overall characteristics of a run is the
RMS of the GTK 1 hits per trigger calculated per burst (see Section 2 Fig. 3a ).
This is shown in Fig. 7 for four runs. Here a high-pass filtered RMS is plotted
against burst number.
High RMS bursts are evident in three runs. A detailed study shows that the high-RMS
bursts are primarily due to 100 Hz and 50 Hz noise for runs 12288 and 13362, respectively.
6) Summary and conclusions.
-----------------------
Bursts with a high intensity component have a high RMS, low SDF and
high skewness of the GTK1 distribution and are identifiable using these and other BQIs.
Since the NA62 trigger is paralyzable there is little dependence of the
number of pnunu events on beam intensity. In contrast, the upstream
background and pileup are at least proportional to the beam intensity.
Consequently, if it is desired to minimimise the background in the event selection,
the BQI introduced here would provide the opportunity to do so.
Addendum 1
--------
Additional BQI plots for SDF, skewness, % greater than 100, mean and RMS for GTK1






 Addemdum 2
---------
Plots for max vs spill time of max.
Plots for mean, rms.
Addemdum 2
---------
Plots for max vs spill time of max.
Plots for mean, rms.








