Exclusive Production of Vector Mesons

The experimental signals are the exclusive production of the vector mesons in the following decay modes:

First results on and higher vector mesons ( and ) are in the early analysis stages and first candidates for are also appearing in the data.

The clean topology of these events results in typical errors on the measured quantities (t, M², W² and Q²), reconstructed in the tracking chambers, of order 5%. Containment within the tracking chambers corresponds to a W interval in the range  GeV. However, some analyses are restricted to a reduced range of W where the tracking and trigger systematics are well understood. Conversely, H1 have also used the shifted vertex data to extend the analysis of the cross section to higher  GeV. At small t there are problems triggering and, to a lesser extent, reconstructing the decay products of the vector meson. In particular, the photoproduction of mesons is limited to  GeV², since the produced kaons are just above threshold and the available energy in the decay is limited. In order to characterise the t-dependence, a fit to the diffractive peak is performed. In the most straightforward approach, a single exponential fit to the t distribution, for GeV² is adopted.

The contributions to the systematic uncertainties are similar in each of the measurements. For example, the uncertainties on acceptance of photoproduced 's are due to uncertainties on trigger thresholds (  9%), variations of the input Monte Carlo distributions (  9%) and track reconstruction uncertainties especially at low p_T (  6%). In particular for the analysis, where the mass distribution is skewed compared to a Breit-Wigner shape, uncertainties arise due to the assumptions of the fit for the interference between the resonant signal and the non-resonant background contributions (  7%). Other significant contributions to the uncertainty are contamination due to e-gas interactions (  2-5%) and from higher mass dissociated photon states, such as elastic and decays (  2-7%). The uncertainty due to neglecting radiative corrections can also be estimated to be 4-5% [7, 8].

Finally, one of the key problems in obtaining accurate measurements of the exclusive cross sections and the t slopes is the uncertainty on the double dissociation component, where the proton has also dissociated into a low mass nucleon system [14]. The forward calorimeters will see the dissociation products of the proton if the invariant mass of the nucleon system, M_N, is above approximately 4 GeV. A significant fraction of double dissociation events produce a limited mass system which is therefore not detected. Proton remnant taggers are now being used further down the proton beamline to provide constraints on this fraction and, in the H1 experiment, further constraints are provided by measuring secondary interactions in the forward muon system. Based on data one finds that the dissociated mass spectrum falls as dN/dM_N² = 1/M_Nⁿ with n = 2.20 0.03 at  GeV from CDF measurements [15]. However it should be noted that this measurement corresponds to a restricted mass interval. The extrapolation to lower masses is subject to uncertainties and the universality of this dissociation is open to experimental question, given the different behaviour at the upper vertex. Precisely how the proton dissociates and whether the proton can be regarded as dissociating independently of the photon system is not a priori known. Currently, this uncertainty is reflected in the cross sections by allowing the value of n to vary from around 2 to 3, although this choice is somewhat arbitrary. The magnitude of the total double dissociation contribution is estimated to be typically prior to cuts on forward energy deposition, a value which can be cross-checked in the data with an overall uncertainty of which is due to the considerations above. Combining the above uncertainties, the overall systematic errors in the various cross sections are typically .

Photoproduction processes have been extensively studied in fixed-target experiments, providing a large range in W over which to study the cross sections. The key features are the weak dependence of the cross section on W, an exponential dependence on t with a slope which shrinks with increasing W and the retention of the helicity of the photon by the vector meson. The t dependence of the photoproduction data is illustrated in Figure 2 where the H1 and ZEUS data are compared to a compilation of lower energy data [16]. The data are consistent with a shrinkage of the t slope with increasing , where is the photon energy in the proton rest frame, as indicated by the curve for soft pomeron exchange [17].

 
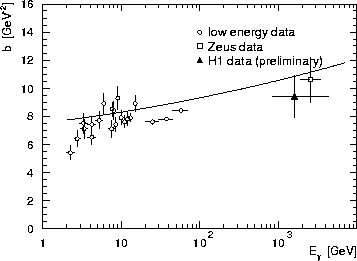
Figure 2: Dependence of the exponential slope parameter b as a function of for exclusive photoproduction compared to the soft pomeron exchange prediction of Schuler and Sjöstrand.

The measured t slopes are  GeV^-2 (H1) [7] and  GeV^-2 (ZEUS) [8] for the (where similar single-exponential fits have been applied). These values can be compared to  GeV^-2 (ZEUS) [10] for the and  GeV^-2 (H1) [13] for the . Physically, the slope of the t dependence in diffractive interactions tells us about the effective radius of that interaction, R: if d , then b 1/4 R². The range of measured b slopes varies from around 4 GeV^-2 (  fm) to 10 GeV^-2 (  fm). Further, the interaction radius can be approximately related to the radii of the interacting proton and vector meson, . Given  fm, then this variation in b slopes corresponds to a significant change in the effective radius of the interacting vector meson from  fm to  fm.

 
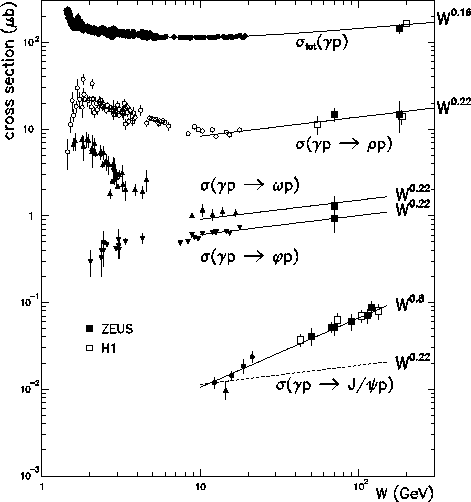
Figure 3: W dependence of the exclusive vector meson and total photoproduction cross sections compared to various power law dependences discussed in the text.

Integrating over the measured t dependence, the W dependence of the results on exclusive vector meson photoproduction cross sections are shown in Figure 3 [18]. From the experimental perspective, there is generally good agreement on the measured cross sections. The total cross section is also shown in Figure 3, rising with increasing energy as in hadron-hadron collisions and consistent with a value of i.e. the total cross section increases as W^0.16.

Given the dominance of the pomeron trajectory at high W and an approximately exponential behaviour of the |t| distribution with slope , whose mean value is given by 1/b, the diffractive cross section rise is moderated from

to

Here characterises the effective energy dependence after integration over t. The observed shrinkage of the diffractive peak therefore corresponds to a relative reduction of the diffractive cross section with increasing energy. Such a dependence describes the general increase of the , and vector meson cross sections with increasing W. However, the rise of the cross section is clearly not described by such a W dependence, the increase being described by an effective W^0.8 dependence. Whilst these effective powers are for illustrative purposes only, it is clear that in exclusive production a new phenomenon is occurring.

Qualitatively, the W^0.8 dependence, corresponding to , could be ascribed to the rise of the gluon density observed in the scaling violations of F₂. The mass scale, M², is larger than the QCD scale , and it is therefore possible to apply pQCD techniques. Quantitatively, the theoretical analysis predicts that the rise of the cross section is proportional to the square of the gluon density at small-x and allows discrimination among the latest parametrisations of the proton structure function [19]. We also know from measurements of the DIS total cross section that application of formula (1) results in a value of which increases with increasing Q², with 0.2 to 0.25 at  GeV² [18]. The fact that the corresponding relative rise of F₂ with decreasing x can be described by pQCD evolution [20] points towards a calculable function for GeV².

One contribution to the DIS total cross section is the electroproduction of low mass vector mesons. Experimentally, the statistical errors typically dominate with systematic uncertainties similar to the photoproduction case. The trigger uncertainties are significantly reduced, however, since the scattered electron is easily identified and the radiative corrections, which are more significant (  [21]), can be corrected for. The W dependence of the DIS and cross sections for finite values of Q² are shown in Figure 4, compared to the corresponding photoproduction cross sections. The W dependence for the and electroproduction data are similar to those for the photoproduction data, consistent with an approximate W^0.8 dependence also shown in Figure 4. An important point to emphasise here is that the relative production of to mesons approaches the quark model prediction of 2/9 at large W and large Q², which would indicate the applicability of pQCD to these cross sections. The measurements of the helicity angle of the vector meson decay provide a measurement of for the (virtual) photon, assuming s-channel helicity conservation, i.e. that the vector meson preserves the helicity of the photon. The photoproduction measurements for the are consistent with the interaction of dominantly transversely polarised photons (  (ZEUS) [8]). However, adopting the same analysis for virtual photons, R=1.5^+2.8_-0.6 (ZEUS) [8], inconsistent with the behaviour in photoproduction and consistent with a predominantly longitudinal exchange. This predominance is expected for an underlying interaction of the virtual photon with the constituent quarks of the . Also, the measured b slope approximately halves from the photoproduction case to a value of  (ZEUS) [8], comparable to that in the photoproduced case. The basic interaction is probing smaller distances, which allows a first comparison of the observed cross section with the predictions of leading-log pQCD (see [8]).

 
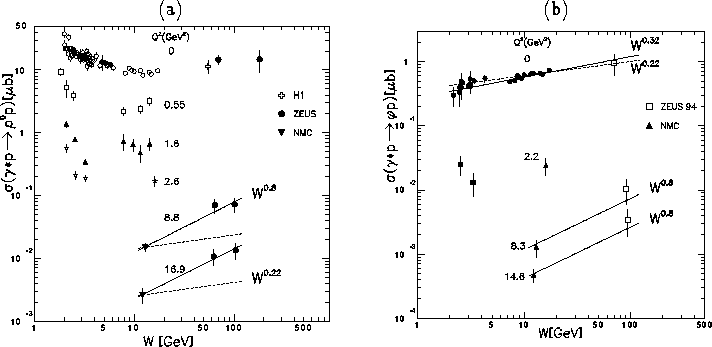
Figure 4: W dependence of exclusive (a) and (b) electroproduction cross sections for fixed values of Q² compared to various power law dependences discussed in the text.

Finally, first results based on the observation of 42 events at significant  GeV² have been reported by H1 [13]. The cross section has been evaluated in two W intervals in order to obtain an indication of the W dependence, as shown in Figure 5, where an estimated 50% contribution due to double dissociation has been subtracted [22]. The electroproduction data are shown with statistical errors only although the systematics are estimated to be smaller than these errors ( ). The electroproduction and photoproduction data are consistent with the W^0.8 dependence ( ) noted previously. The electroproduction cross section is of the same order of that of the data, in marked contrast to the significantly lower photoproduction cross section for the , even at HERA energies, also shown in Figure 5. Further results in this area would allow tests of the underlying dynamics for transverse and longitudinally polarised photons coupling to light and heavy quarks in the pQCD calculations.

 
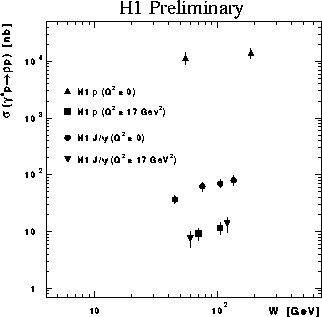
Figure 5: H1 measurements of the W dependence of electroproduction and photoproduction cross sections of exclusive vector mesons.

In conclusion, there is an accumulating body of exclusive vector meson production data, measured with a systematic precision of , which exhibit two classes of W² behaviour: a slow rise consistent with that of previously measured diffractive data for low M² photoproduction data but a significant rise of these cross sections when a finite Q² and/or a significant M² is measured.