Deep Inelastic Structure of Diffraction

One of the major advances in the subject of diffraction has been the observation of large rapidity gap events in DIS and their subsequent analysis in terms of a diffractive structure function [23, 24]. In these analyses, the signature of diffraction is the rapidity gap, defined by measuring the maximum pseudorapidity of the most-forward going particle with energy above 400 MeV, , and requiring this to be well away from the outgoing proton direction. A typical requirement of corresponds to a low mass state measured in the detectors of units and a large gap of units with respect to the outgoing proton (nucleon system). In order to increase the lever arm in M², the H1 and ZEUS analyses have extended the cuts to 3.2 and 2.5, respectively. This is achieved directly using the forward muon system/proton remnant taggers, in the case of H1, or via the measurement of a further discriminating variable, , where is the momentum vector of a calorimeter cell, for ZEUS. These extensions are, however, at the expense of a significant non-diffractive DIS background (up to and , respectively). In each case, this background is estimated using the the colour-dipole model as implemented in the ARIADNE 4.03 program [26], which reasonably reproduces the observed forward E_T flows in non-diffractive interactions. The uncertainty on this background is estimated by changing the applied cuts or by using other Monte Carlo models and is up to 20% for large masses, M², of the dissociated photon. The double dissociation contribution is estimated with similar uncertainties to the vector meson case. Other systematic errors are similar to those for the F₂ analyses ( ) with additional acceptance uncertainties due to variations of the input diffractive Monte Carlo distributions.

In the presentation of the results, the formalism changes [25], reflecting an assumed underlying partonic description, and two orthogonal variables are determined:

the momentum fraction of the pomeron within the proton and the momentum fraction of the struck quark within the pomeron, respectively. The structure function is then defined by analogy to that of the total ep cross section:

where the contribution of F_L and radiative corrections are neglected and an integration over the (unmeasured) t variable is performed. The effect of neglecting F_L corresponds to a relative reduction of the cross section at small  (high W²) which is always and therefore smaller than the typical measurement uncertainties ( ).

As discussed above, a major uncertainty comes from the estimation of the non-diffractive background. This problem has been addressed in a different way in a further analysis by ZEUS [27]. In this analysis the mass spectrum, M², is measured as a function of W and Q², as shown in Figure 6 for four representative intervals, where the measured mass is reconstructed in the calorimeter and corrected for energy loss but not for detector acceptance, resulting in the turnover at large M². The diffractive data are observed as a low mass shoulder at low W, which becomes increasingly apparent at higher W. Also shown in the figure are the estimates of the non-diffractive background based on (a) the ARIADNE Monte Carlo (dotted histogram) and (b) a direct fit to the data, discussed below.

 
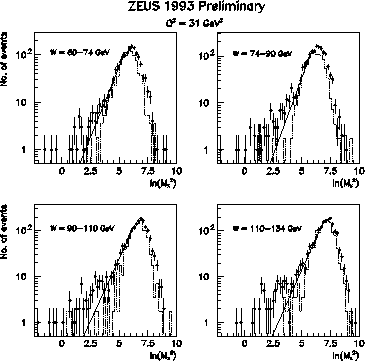
Figure: Preliminary ZEUS analysis of the distributions as a function of W at Q² = 31 GeV². The solid lines show the extrapolation of the nondiffractive background as determined by the fits discussed in the text. The dotted histograms show the predictions for non-diffractive scattering as modelled using the ARIADNE 4.03 program.

The probability of producing a gap is exponentially suppressed as a function of the rapidity gap, and hence as a function of ), for non-diffractive interactions. The slope of this exponential is directly related to the height of the plateau distribution of multiplicity in the region of rapidity where the subtraction is made. The data can thus be fitted to functions of the form , in the region where the detector acceptance is uniform, where b, C and D are determined from the fits. Here, D represents a first-order estimate of the diffractive contribution which is flat in ). The important parameter is b, which is determined to be in fits to each of the measured data intervals, compared to estimated from the ARIADNE Monte Carlo. The systematic uncertainty in the background reflects various changes to the fits, but in each case the measured slope is incompatible with that of the Monte Carlo. This result in itself is interesting, since the fact that ARIADNE approximately reproduces the observed forward E_T ( multiplicity) flow but does not reproduce the measured b slope suggests that significantly different correlations of the multiplicities are present in non-diffractive DIS compared to the Monte Carlo expectations. Also new in this analysis is that the diffractive Monte Carlo POMPYT 1.0 [28] has been tuned to the observed data contribution for low mass states, allowing the high region to be measured up to the kinematic limit ( ) and radiative corrections have been estimated in each interval (  [21]).

The virtual-photon proton cross sections measured at fixed M² and W, measured in this analysis, can be converted to F₂^D(3) at fixed and . These results are shown in Figure 7 as the ZEUS(BGD) [27] analysis, compared to the earlier H1 [23] and ZEUS(BGMC) [24] analyses in comparable intervals of and Q² as a function of . The overall cross sections in each and Q² interval are similar, however, the  dependences are different. As can be seen in Figure 6, the background estimates are significantly different which results in a systematic shift in the W ( ) dependence at fixed M ( ) and Q².

 
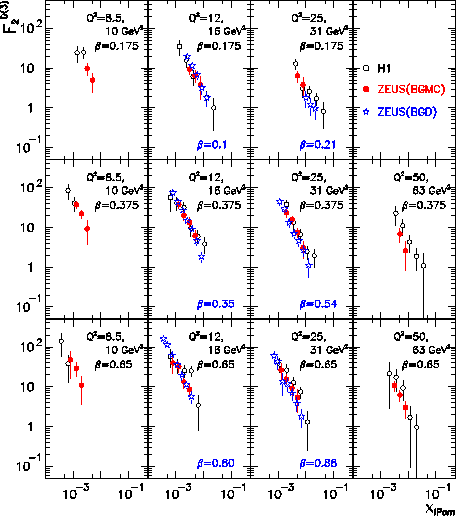
Figure 7: Comparison of the HERA data for F₂^D(3) as function of for the H1 and ZEUS(BGMC) analyses where the Monte Carlos are used to estimate the background. The upper (lower) Q² value refers to the H1 (ZEUS) analysis. The preliminary ZEUS(BGD) where a fit to the data is used to estimate the non-diffractive background is compared at slightly different values noted at the bottom of the figure.

Fits of the form are performed where the normalisation constants b_i are allowed to differ in each interval. The fits are motivated by the factorisable ansatz of where measures the flux of pomerons in the proton and is the probed structure of the pomeron. The exponent of  is identified as , where measures the effective  dependence ( dependence at fixed M² and Q²) of the cross section, integrated over t, as discussed in relation to exclusive vector meson production. In each case, the are indicating that a single power law dependence on energy provides a reasonable description of the data and that effects due to factorisation breaking predicted in QCD-based calculations [29] are not yet observable. The results for are  (H1) [23],  (ZEUS(BGMC)) [24] and  (ZEUS(BGD)) [27], where the systematic errors are obtained by refitting according to a series of systematic checks outlined above. It should be noted that the (2 ) systematic shift between the ZEUS(BGD) and ZEUS(BGMC) can be attributed to the method of background subtraction. Whilst the H1 and ZEUS(BGMC) analyses, based on Monte Carlo background subtraction, agree within errors, the ZEUS(BGD) value is different from the H1 value at the 3 level.

The Donnachie-Landshoff prediction [3] is , after integration over an assumed t dependence and taking into account shrinkage. While comparison with the H1 value indicates that this contribution is significant, the possibility of additional contributions cannot be neglected. Taking the ZEUS(BGD) value, this measurement is incompatible with the predicted soft pomeron behaviour at the 4 level. Estimates of the effect of made by assuming rather than result in increasing from 0.24 to 0.29.

The values can also be compared with 0.2 obtained from the exclusive photoproduction of mesons and the electroproduction data or with 0.2 to 0.25 obtained from the dependence of the total cross sections in the measured Q² range [18]. In the model of Buchmüller and Hebecker [30], the effective exchange is dominated by one of the two gluons. In terms of , where the optical theorem is no longer relevant, the diffractive cross section would therefore rise with an effective power which is halved to 0.1 to 0.125. The measured values are within the range of these estimates.

The overall cross sections in each , Q² interval are similar and one can integrate over the measured  dependence in order to determine ( ), a quantity which measures the internal structure of the pomeron up to an arbitrary integration constant. Presented in this integrated form, the data agree on the general features of the internal structure. In Figure 8 the H1 data are compared to preliminary QCD fits [31]. The general conclusions from the dependence are that the pomeron has a predominantly hard structure, typically characterised by a symmetric dependence, but also containing an additional, significant contribution at low which has been fitted in the ZEUS analysis [24]. The virtual photon only couples directly to quarks, but the overall cross section can give indications only of the relative proportion of quarks and gluons within the pomeron, since the flux normalisation is somewhat arbitrary [24]. The Q² behaviour is broadly scaling, consistent with a partonic structure of the pomeron. Probing more deeply, however, a characteristic logarithmic rise of is observed in all intervals. Most significantly, at large a predominantly quark-like object would radiate gluons resulting in negative scaling violations as in the case of the large-x ( ) behaviour of the proton. The question of whether the pomeron is predominantly quarks or gluons, corresponding to a ``quarkball" or a ``gluemoron" [32], has been tested quantitatively by H1 using QCD fits to  [31]. A flavour singlet quark density input of the form , where z is the momentum fraction carried by the quark, yields a numerically acceptable . The characteristic Q² behaviour, however, is not reproduced. Adding a gluon contribution of similar form gives an excellent description of the data. The fit shown uses B_q = 0.35, C_q = 0.35, B_g = 8, C_g = 0.3. In general, the fits tend to favour inputs where the gluon carries a significant fraction, 70 to 90%, of the pomeron's momentum.

 
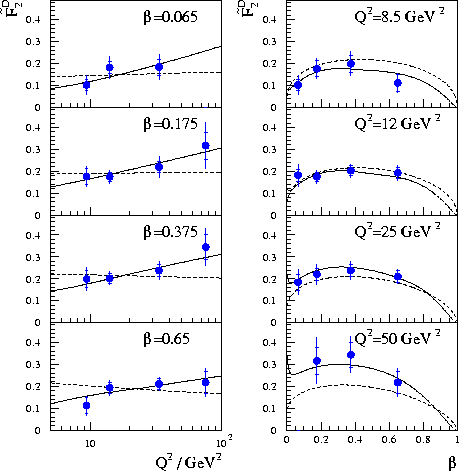
Figure: H1 data on ( ) as a function of Q² ( ) at fixed (Q²). The data are compared to preliminary leading-order QCD fits where: (a) only quarks are considered at the starting scale, Q₀² = 4 GeV², indicated by the dashed line ( , 37% CL); (b) gluons also contribute at the starting scale, resulting in a fit where gluons carry 90% of the momentum, indicated by the full line ( , 91% CL).