

Next: Conclusions and Outlook
Up: Rapidity Gaps in Hard
Previous: Central Rapidity Gaps
The class of events which will be discussed in this section exhibits a
rapidity gap extending to high values of 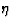 . An example is shown in
Figure 9.
. An example is shown in
Figure 9.
Figure:
A hard photoproduction event with a foward gap. The z-R display
of the ZEUS detector is shown on the left hand side. In the
upper right hand corner the 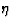 and
and 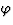 coordinates of the
calorimeter energy deposits are shown, weighted by their transverse
energy. The lower right hand view is the x-y cross section.
coordinates of the
calorimeter energy deposits are shown, weighted by their transverse
energy. The lower right hand view is the x-y cross section.
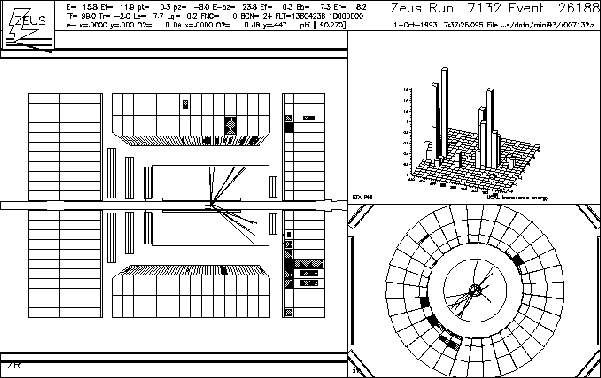 |
There are two high transverse energy jets which are back to back in 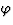 and no scattered e- candidate. This is a hard photoproduction
event. However there is no energy in the forward direction around the
beam pipe which could be associated with the fragmentation products of the
proton remnant. This is, therefore, a candidate diffractive hard scattering
event.
and no scattered e- candidate. This is a hard photoproduction
event. However there is no energy in the forward direction around the
beam pipe which could be associated with the fragmentation products of the
proton remnant. This is, therefore, a candidate diffractive hard scattering
event.
This analysis proceeds in a similar way to that described in the previous
section. First the uncorrected data are compared to Monte Carlo generated
event samples which have been subjected to a full simulation of the ZEUS
detector. In a second step the generated event samples are used to correct
the data for the effects of the detector smearing and acceptance. Again,
specific details of the analysis should be obtained from the
publication [2].
The diffractive hard scattering process is understood to proceed as
illustrated in Figure 10(a) where we have introduced two new momentum
fraction variables. 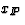 represents the fraction of the proton's
momentum which is carried by the pomeron and
represents the fraction of the proton's
momentum which is carried by the pomeron and 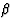 represents the fraction
of the pomeron's momentum which is carried into the hard subprocess. Of
course
represents the fraction
of the pomeron's momentum which is carried into the hard subprocess. Of
course 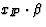 gives the familiar Bjorken-xp variable.
gives the familiar Bjorken-xp variable.
Figure:
Kinematics of the diffractive hard photoproduction process.
The meaning of the momentum fraction variables 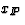 and
and
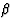 is illustrated in (a) where the fraction of the photon's
momentum entering the hard subprocess,
is illustrated in (a) where the fraction of the photon's
momentum entering the hard subprocess, 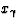 , the photon
virtuality, P2, and the squared momentum transfer which sets the
energy scale of the hard subprocess,
Q2, are also indicated. The pseudorapidity of the particle with
the highest pseudorapidity is denoted
, the photon
virtuality, P2, and the squared momentum transfer which sets the
energy scale of the hard subprocess,
Q2, are also indicated. The pseudorapidity of the particle with
the highest pseudorapidity is denoted 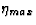 as illustrated
in (b).
as illustrated
in (b).
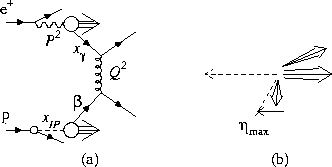 |
The other important variable for describing the diffractive hard
photoproduction process is  .
. 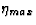 is defined to be the
pseudorapidity of the most forward going particle (measured using the
calorimeter) which has energy exceeding 400 MeV. The definition of
is defined to be the
pseudorapidity of the most forward going particle (measured using the
calorimeter) which has energy exceeding 400 MeV. The definition of
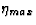 is illustrated schematically in Figure 10(b).
is illustrated schematically in Figure 10(b).
The 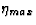 distribution for a sample of hard photoproduction events
is shown in Figure 11. For this particular plot a subsample
of events is shown for which the total hadronic invariant mass, MX,
(measured using all of the energy deposits in the calorimeter) satisfies
MX < 30 GeV.
The data are shown by black dots and are
not corrected for detector effects. The errors shown are statistical only.
The data are peaked toward a value of
distribution for a sample of hard photoproduction events
is shown in Figure 11. For this particular plot a subsample
of events is shown for which the total hadronic invariant mass, MX,
(measured using all of the energy deposits in the calorimeter) satisfies
MX < 30 GeV.
The data are shown by black dots and are
not corrected for detector effects. The errors shown are statistical only.
The data are peaked toward a value of 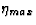 which is close to the
edge of the calorimeter acceptance. However there is a large contribution
which is close to the
edge of the calorimeter acceptance. However there is a large contribution
Figure:
The 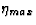 distribution for a sample of hard photoproduction
events. The data are shown by black dots
with error bars representing statistical errors only. No corrections
for detector effects have been made. The shaded histogram shows
the prediction from the PYTHIA standard hard photoproduction events.
The open histogram shows the prediction from the POMPYT
simulation of
distribution for a sample of hard photoproduction
events. The data are shown by black dots
with error bars representing statistical errors only. No corrections
for detector effects have been made. The shaded histogram shows
the prediction from the PYTHIA standard hard photoproduction events.
The open histogram shows the prediction from the POMPYT
simulation of 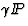 scattering where the
scattering where the 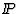 contains
a hard gluon spectrum (see text). The Monte Carlo event samples
have been subjected to a full simulation of the detector acceptance
and smearing.
contains
a hard gluon spectrum (see text). The Monte Carlo event samples
have been subjected to a full simulation of the detector acceptance
and smearing.
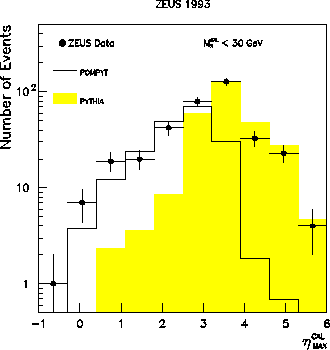 |
from events with very low values of 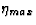 , indicating the presence of
a forward rapidity gap. Also shown in this figure are two Monte Carlo
predictions which include a full simulation of the ZEUS detector. The
shaded histogram shows the PYTHIA prediction for standard hard photoproduction
processes. It fails to describe the large rapidity gap events of the data
which occur at low values of
, indicating the presence of
a forward rapidity gap. Also shown in this figure are two Monte Carlo
predictions which include a full simulation of the ZEUS detector. The
shaded histogram shows the PYTHIA prediction for standard hard photoproduction
processes. It fails to describe the large rapidity gap events of the data
which occur at low values of 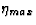 . To describe these large rapidity
gap events we must introduce the Monte Carlo program POMPYT [18],
the prediction of which is shown by the open histogram.
. To describe these large rapidity
gap events we must introduce the Monte Carlo program POMPYT [18],
the prediction of which is shown by the open histogram.
POMPYT is a Monte Carlo implementation of the Ingelman-Schlein
model [19] which assumes that the hard photoproduction
cross section 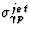 factorizes in the following way.
factorizes in the following way.
| 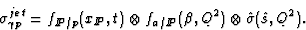 |
(1) |
In words, the jet cross section, 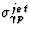 , may be written
as the convolution of a term representing the flux of pomerons in the
proton,
, may be written
as the convolution of a term representing the flux of pomerons in the
proton, 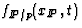 , with a term describing the
flux of partons in the pomeron,
, with a term describing the
flux of partons in the pomeron, 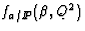 , and with
the subprocess cross section,
, and with
the subprocess cross section, 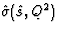 .The direct photoproduction subprocess cross section includes only the hard
subprocesses,
.The direct photoproduction subprocess cross section includes only the hard
subprocesses, 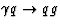 and
and 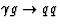 .In resolved photoproduction it includes in addition to
the hard subprocesses
.In resolved photoproduction it includes in addition to
the hard subprocesses 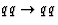 ,
, 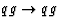 , etcetera,
the flux of partons in the photon,
, etcetera,
the flux of partons in the photon, 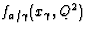 .The hard subprocess cross sections are calculable in perturbative QCD and
some experimental information exists which constrains the
.The hard subprocess cross sections are calculable in perturbative QCD and
some experimental information exists which constrains the
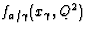 . Therefore
. Therefore 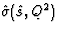 is
a known input in Eqn. 1. The pomeron flux factor,
is
a known input in Eqn. 1. The pomeron flux factor,
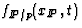 , may be
determined using Regge inspired fits to hadron-hadron data.
The remaining unknown ingredient is the pomeron structure. We neglect
the energy scale dependence of
, may be
determined using Regge inspired fits to hadron-hadron data.
The remaining unknown ingredient is the pomeron structure. We neglect
the energy scale dependence of 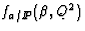 and consider
two extreme possibilities for its
and consider
two extreme possibilities for its 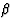 dependence.
The first,
dependence.
The first, 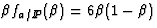 , yields
a mean
, yields
a mean 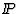 momentum fraction of
momentum fraction of 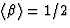 and
is therefore known as the hard parton density.
The second,
and
is therefore known as the hard parton density.
The second, 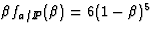 , has
, has
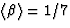 and is called the soft parton density.
Finally, it is not clear whether there should be a momentum sum rule
for the pomeron, that is, whether
and is called the soft parton density.
Finally, it is not clear whether there should be a momentum sum rule
for the pomeron, that is, whether
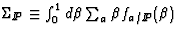 must equal 1 or not.
must equal 1 or not.
The open histogram in Figure 11 shows the POMPYT prediction for
a 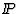 consisting entirely of gluons with the hard momentum spectrum.
A fairly satisfactory description of
consisting entirely of gluons with the hard momentum spectrum.
A fairly satisfactory description of 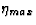 may be achieved. In
addition
the POMPYT prediction is able to describe the MX distribution, and
the distribution of the photon proton centre-of-mass energies,
may be achieved. In
addition
the POMPYT prediction is able to describe the MX distribution, and
the distribution of the photon proton centre-of-mass energies,
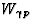 , for rapidity gap events with
, for rapidity gap events with 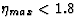 .(The results are similar for a
.(The results are similar for a 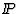 composed entirely of hard quarks.)
For this reason we say that the data are consistent with containing a
contribution from diffractive hard photoproduction processes.
composed entirely of hard quarks.)
For this reason we say that the data are consistent with containing a
contribution from diffractive hard photoproduction processes.
In the second step of the analysis we correct the data for all effects of
detector acceptance and smearing. We present in Figure 12 the
ep cross section for photoproduction of jets of ETjet > 8 GeV
as a function of the jet pseudorapidity.
This cross section is for events which have a rapidity gap characterized
by 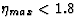 .
.
Figure:
Cross section 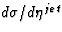 for photoproduction of jets
with ETjet > 8 GeV in events with
for photoproduction of jets
with ETjet > 8 GeV in events with 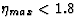 . The
inner error bars show the statistical errors and the outer error bars
the systematic uncertainty added in quadrature -- excluding the
systematic uncertainty due to the calorimeter energy scale which is
shown by
the shaded band. The PYTHIA prediction for standard hard
photoproduction processes is shown by the dashed line. The POMPYT
predictions
. The
inner error bars show the statistical errors and the outer error bars
the systematic uncertainty added in quadrature -- excluding the
systematic uncertainty due to the calorimeter energy scale which is
shown by
the shaded band. The PYTHIA prediction for standard hard
photoproduction processes is shown by the dashed line. The POMPYT
predictions 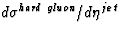 ,
, 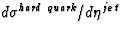 and
and
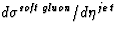 for diffractive hard processes with different
parton distribution functions and
for diffractive hard processes with different
parton distribution functions and 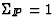 are shown by
the solid lines.
are shown by
the solid lines.
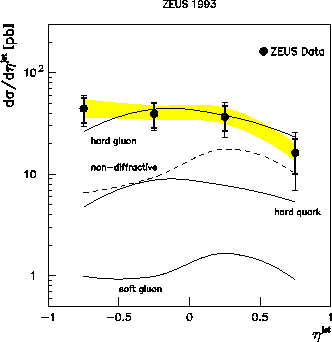 |
The PYTHIA prediction for this cross section for non-diffractive processes
is shown by the dashed line. It is too low in overall magnitude to describe
the data as well as being disfavoured in shape. The POMPYT predictions,
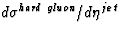 ,
,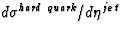 and
and
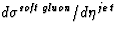 for the hard gluon, the hard quark and the soft gluon pomeron parton
densities respectively where
for the hard gluon, the hard quark and the soft gluon pomeron parton
densities respectively where 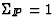 are shown by the
solid curves.
The soft parton density very rarely gives rise to sufficient momentum transfer
to produce two ETjet > 8 GeV jets and so
are shown by the
solid curves.
The soft parton density very rarely gives rise to sufficient momentum transfer
to produce two ETjet > 8 GeV jets and so
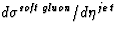 lies far below the cross sections for the hard parton densities
in overall normalization.
lies far below the cross sections for the hard parton densities
in overall normalization.
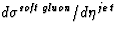 is inconsistent
with the data in overall magnitude as well as being disfavoured in shape.
We do not consider soft parton densities further.
is inconsistent
with the data in overall magnitude as well as being disfavoured in shape.
We do not consider soft parton densities further.
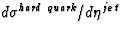 is consistent with the data in shape but too small in
magnitude.
is consistent with the data in shape but too small in
magnitude.
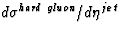 is capable of describing both the shape
and magnitude of the measured cross section.
Note, however, that the non-diffractive contribution to the data has not been
subtracted, nor has the double dissociation contribution.
is capable of describing both the shape
and magnitude of the measured cross section.
Note, however, that the non-diffractive contribution to the data has not been
subtracted, nor has the double dissociation contribution.
In the final stage of the analysis the non-diffractive contribution was
subtracted from the data using the PYTHIA prediction (which has been
shown to provide a good description of inclusive jet cross sections
in photoproduction [20]).
A contribution
of 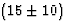 % due to double dissociation processes was also subtracted.
Then the assumption that
% due to double dissociation processes was also subtracted.
Then the assumption that 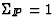 was relaxed. The
was relaxed. The 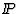 was assumed to be composed of a fraction cg of hard gluons and a fraction
1-cg of hard quarks.
Then for various values of cg the expression
was assumed to be composed of a fraction cg of hard gluons and a fraction
1-cg of hard quarks.
Then for various values of cg the expression
![$\Sigma_{I\!\!P} \cdot
[ c_g \cdot d\sigma^{\mbox{\scriptsize\it hard gluon}}/...
...et}
+ (1-c_g) \cdot d\sigma^{\mbox{\scriptsize\it hard quark}}/d\eta^{jet} ] $](img82.gif) was fit to the measured
was fit to the measured 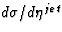 distribution to obtain
distribution to obtain
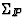 . (The POMPYT predictions for
. (The POMPYT predictions for
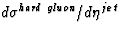 and
and
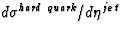 were used in the
fit.)
The result of this series of fits is shown in Figure 13 by the
solid line where the statistical uncertainty of the fit is indicated by the
shaded band.
were used in the
fit.)
The result of this series of fits is shown in Figure 13 by the
solid line where the statistical uncertainty of the fit is indicated by the
shaded band.
Figure:
Allowed regions of the 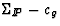 plane. The solid
line and its shaded band of uncertainty show the constraint from
the measurement of
plane. The solid
line and its shaded band of uncertainty show the constraint from
the measurement of 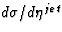 . The
dash-dotted lines and their shaded band of uncertainty show the
constraint imposed from the measurement of F2D(3). (The upper
dash-dotted curve is for two quark flavours and the lower
dash-dotted curve is for three quark flavours.)
. The
dash-dotted lines and their shaded band of uncertainty show the
constraint imposed from the measurement of F2D(3). (The upper
dash-dotted curve is for two quark flavours and the lower
dash-dotted curve is for three quark flavours.)
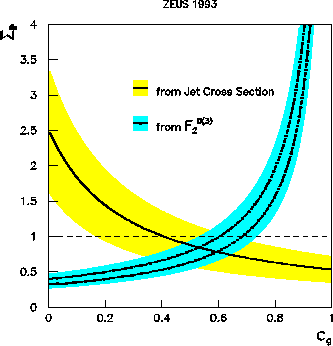 |
We find, for instance, that the data are do not favour a 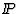 which
consists exclusively of hard gluons and simultaneously satisfies
the momentum sum rule,
which
consists exclusively of hard gluons and simultaneously satisfies
the momentum sum rule, 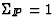 . (See [2], however,
for a discussion of additional theoretical systematic uncertainties.)
. (See [2], however,
for a discussion of additional theoretical systematic uncertainties.)
Results from studies of diffractive hard electroproduction have
been expressed in terms of the diffractive structure function,
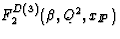 [21,22]. The expression of
factorization is then,
[21,22]. The expression of
factorization is then,
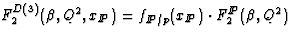 .Integrating this over
.Integrating this over 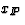 and
and
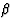 and then subtracting
the integral over the pomeron flux
thus gives the sum of the momenta of all of the quarks in the pomeron,
and then subtracting
the integral over the pomeron flux
thus gives the sum of the momenta of all of the quarks in the pomeron,
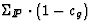 .The ZEUS measurement [22],
.The ZEUS measurement [22],
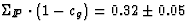 , is shown in
Figure 13 by the lower dot-dashed line. This is the result for
two flavours of quark in the
, is shown in
Figure 13 by the lower dot-dashed line. This is the result for
two flavours of quark in the 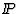 . The result for three flavours
of quark is
. The result for three flavours
of quark is 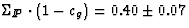 , the upper
dot-dashed line in Figure 13. The dark-shaded band shows the
additional measurement uncertainty.
, the upper
dot-dashed line in Figure 13. The dark-shaded band shows the
additional measurement uncertainty.
Assuming that the pomeron flux is the same in the measurement of
F2D(3) and of 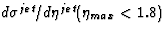 one can combine the two analyses to determine the allowed ranges,
one can combine the two analyses to determine the allowed ranges,
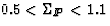 and 0.35 < cg < 0.7. However the
and 0.35 < cg < 0.7. However the
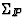 range is affected by additional uncertainties in the
normalization of the pomeron flux factor. Taking into account all remaining
systematic uncertainties of the measurements we find 0.3 < cg < 0.8.
This measurement is independent of the pomeron flux and of the total momentum
carried by partons in the pomeron.
range is affected by additional uncertainties in the
normalization of the pomeron flux factor. Taking into account all remaining
systematic uncertainties of the measurements we find 0.3 < cg < 0.8.
This measurement is independent of the pomeron flux and of the total momentum
carried by partons in the pomeron.
In summary, the distributions of 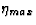 , MX and
, MX and 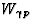 indicate that the events with a forward rapidity gap are consistent with
a diffractive hard scattering via exchange of a low-t pomeron.
The ep cross section
indicate that the events with a forward rapidity gap are consistent with
a diffractive hard scattering via exchange of a low-t pomeron.
The ep cross section 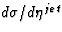 for the photoproduction of
jets of ETjet > 8 GeV in large rapidity gap events (
for the photoproduction of
jets of ETjet > 8 GeV in large rapidity gap events (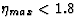 )has been measured and is significantly larger than the cross section due to
non-diffractive processes. A comparison of the
)has been measured and is significantly larger than the cross section due to
non-diffractive processes. A comparison of the 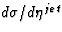 measurement in
photoproduction with the measurement of F2D(3) in electroproduction
indicates that 30% to 80% of the momentum of the pomeron which is due
to partons is carried by hard gluons.
measurement in
photoproduction with the measurement of F2D(3) in electroproduction
indicates that 30% to 80% of the momentum of the pomeron which is due
to partons is carried by hard gluons.


Next: Conclusions and Outlook
Up: Rapidity Gaps in Hard
Previous: Central Rapidity Gaps
latex2html conversion by www person on 1997-08-14
![]() . An example is shown in
Figure 9.
. An example is shown in
Figure 9.
![]() represents the fraction of the proton's
momentum which is carried by the pomeron and
represents the fraction of the proton's
momentum which is carried by the pomeron and ![]() represents the fraction
of the pomeron's momentum which is carried into the hard subprocess. Of
course
represents the fraction
of the pomeron's momentum which is carried into the hard subprocess. Of
course ![]() gives the familiar Bjorken-xp variable.
gives the familiar Bjorken-xp variable.
![]() distribution for a sample of hard photoproduction events
is shown in Figure 11. For this particular plot a subsample
of events is shown for which the total hadronic invariant mass, MX,
(measured using all of the energy deposits in the calorimeter) satisfies
MX < 30 GeV.
The data are shown by black dots and are
not corrected for detector effects. The errors shown are statistical only.
The data are peaked toward a value of
distribution for a sample of hard photoproduction events
is shown in Figure 11. For this particular plot a subsample
of events is shown for which the total hadronic invariant mass, MX,
(measured using all of the energy deposits in the calorimeter) satisfies
MX < 30 GeV.
The data are shown by black dots and are
not corrected for detector effects. The errors shown are statistical only.
The data are peaked toward a value of ![]() which is close to the
edge of the calorimeter acceptance. However there is a large contribution
which is close to the
edge of the calorimeter acceptance. However there is a large contribution
![]() factorizes in the following way.
factorizes in the following way.
![]() consisting entirely of gluons with the hard momentum spectrum.
A fairly satisfactory description of
consisting entirely of gluons with the hard momentum spectrum.
A fairly satisfactory description of ![]() may be achieved. In
addition
the POMPYT prediction is able to describe the MX distribution, and
the distribution of the photon proton centre-of-mass energies,
may be achieved. In
addition
the POMPYT prediction is able to describe the MX distribution, and
the distribution of the photon proton centre-of-mass energies,
![]() , for rapidity gap events with
, for rapidity gap events with ![]() .(The results are similar for a
.(The results are similar for a ![]() composed entirely of hard quarks.)
For this reason we say that the data are consistent with containing a
contribution from diffractive hard photoproduction processes.
composed entirely of hard quarks.)
For this reason we say that the data are consistent with containing a
contribution from diffractive hard photoproduction processes.
![]() .
.
![]() % due to double dissociation processes was also subtracted.
Then the assumption that
% due to double dissociation processes was also subtracted.
Then the assumption that ![]() was relaxed. The
was relaxed. The ![]() was assumed to be composed of a fraction cg of hard gluons and a fraction
1-cg of hard quarks.
Then for various values of cg the expression
was assumed to be composed of a fraction cg of hard gluons and a fraction
1-cg of hard quarks.
Then for various values of cg the expression
![]() was fit to the measured
was fit to the measured ![]() distribution to obtain
distribution to obtain
![]() . (The POMPYT predictions for
. (The POMPYT predictions for
![]() and
and
![]() were used in the
fit.)
The result of this series of fits is shown in Figure 13 by the
solid line where the statistical uncertainty of the fit is indicated by the
shaded band.
were used in the
fit.)
The result of this series of fits is shown in Figure 13 by the
solid line where the statistical uncertainty of the fit is indicated by the
shaded band.
![]() [21,22]. The expression of
factorization is then,
[21,22]. The expression of
factorization is then,
![]() .Integrating this over
.Integrating this over ![]() and
and
![]() and then subtracting
the integral over the pomeron flux
thus gives the sum of the momenta of all of the quarks in the pomeron,
and then subtracting
the integral over the pomeron flux
thus gives the sum of the momenta of all of the quarks in the pomeron,
![]() .The ZEUS measurement [22],
.The ZEUS measurement [22],
![]() , is shown in
Figure 13 by the lower dot-dashed line. This is the result for
two flavours of quark in the
, is shown in
Figure 13 by the lower dot-dashed line. This is the result for
two flavours of quark in the ![]() . The result for three flavours
of quark is
. The result for three flavours
of quark is ![]() , the upper
dot-dashed line in Figure 13. The dark-shaded band shows the
additional measurement uncertainty.
, the upper
dot-dashed line in Figure 13. The dark-shaded band shows the
additional measurement uncertainty.
![]() one can combine the two analyses to determine the allowed ranges,
one can combine the two analyses to determine the allowed ranges,
![]() and 0.35 < cg < 0.7. However the
and 0.35 < cg < 0.7. However the
![]() range is affected by additional uncertainties in the
normalization of the pomeron flux factor. Taking into account all remaining
systematic uncertainties of the measurements we find 0.3 < cg < 0.8.
This measurement is independent of the pomeron flux and of the total momentum
carried by partons in the pomeron.
range is affected by additional uncertainties in the
normalization of the pomeron flux factor. Taking into account all remaining
systematic uncertainties of the measurements we find 0.3 < cg < 0.8.
This measurement is independent of the pomeron flux and of the total momentum
carried by partons in the pomeron.
![]() , MX and
, MX and ![]() indicate that the events with a forward rapidity gap are consistent with
a diffractive hard scattering via exchange of a low-t pomeron.
The ep cross section
indicate that the events with a forward rapidity gap are consistent with
a diffractive hard scattering via exchange of a low-t pomeron.
The ep cross section ![]() for the photoproduction of
jets of ETjet > 8 GeV in large rapidity gap events (
for the photoproduction of
jets of ETjet > 8 GeV in large rapidity gap events (![]() )has been measured and is significantly larger than the cross section due to
non-diffractive processes. A comparison of the
)has been measured and is significantly larger than the cross section due to
non-diffractive processes. A comparison of the ![]() measurement in
photoproduction with the measurement of F2D(3) in electroproduction
indicates that 30% to 80% of the momentum of the pomeron which is due
to partons is carried by hard gluons.
measurement in
photoproduction with the measurement of F2D(3) in electroproduction
indicates that 30% to 80% of the momentum of the pomeron which is due
to partons is carried by hard gluons.