Fragmentation Functions

Fragmentation functions represent the probability for a parton to fragment into a particular hadron carrying a certain fraction of the parton's energy. Fragmentation functions incorporate the long distance, non-perturbative physics of the hadronization process in which the observed hadrons are formed from final state partons of the hard scattering process and, like structure functions, cannot be calculated in perturbative QCD, but can be evolved from a starting distribution at a defined energy scale. If the fragmentation functions are combined with the cross sections for the inclusive production of each parton type in the given physical process, predictions can be made for the scaled momentum, x_p, spectra of final state hadrons. Small x_p fragmentation is significantly affected by the coherence (destructive interference) of soft gluons [28], whilst scaling violation of the fragmentation function at large x_p allows a measurement of $\alpha_s$ [29].

In e⁺e^- annihilation the two quarks are produced with equal and opposite momenta, $\pm \sqrt{s}/2.$This can be compared with a quark struck from within the proton with outgoing momentum -Q/2 in the Breit frame. In the direction of the struck quark (the current fragmentation region) the particle momentum spectra, x_p = 2p^B/Q, are expected to have a dependence on Q similar to those observed in e⁺e^- annihilation [30,31,32] at energy $\sqrt{s}=Q.$

The inclusive charged particle distributions [33,34], $(1/\sigma_{tot})d\sigma/d x_p,$ are shown in figure 6 plotted in bins of fixed x_p as a function of Q². For $Q^2 \gt 80{\rm\ GeV^2}$ the distributions rise with Q² at low x_p and fall-off at high x_p and high Q². By measuring the amount of scaling violation one can ultimately measure the amount of parton radiation and thus determine $\alpha_s.$Below $Q^2=80{\rm\ GeV^2}$ the fall off is due to depopulation of the current region.

  

Figure: The inclusive charged particle distribution, $1/\sigma_{tot}~ d\sigma/dx_p$,in the current fragmentation region of the Breit frame compared to the NLO calculation, CYCLOPS [35].

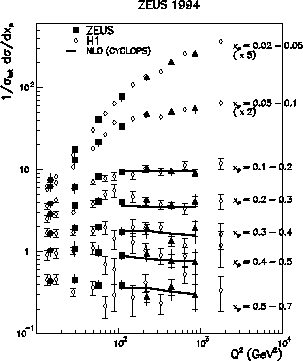The results can be compared to the next-to-leading order (NLO) QCD calculations, as implemented in CYCLOPS [35], of the charged particle inclusive distributions in the restricted region $Q^2 \gt 80{\rm\ GeV^2}$ and x_p > 0.1 , where the theoretical uncertainties are small, unaffected by the hadron mass effects which are not included in the fragmentation function. This comparison is shown in figure 6. The NLO calculation combines a full next-to-leading order matrix element with the ${\rm MRSA^{\prime}}$ parton densities (with a $\Lambda_{\rm QCD} = 230{\rm \ MeV})$and NLO fragmentation functions derived by Binnewies et al. from fits to e⁺e^- data [36]. The data and the NLO calculations are in good agreement, supporting the idea of universality of quark fragmentation.

The peak position of the  distributions, , was evaluated. Figure 7 shows the distribution of  as a function of Q for the HERA data [33,37,38] and of $\sqrt s$ for the e⁺e^- data. Over the range shown the peak moves from $\simeq$ 1.5 to 3.0, equivalent to the position of the maximum of the corresponding momentum spectrum increasing from $\simeq$ 400 to 900 MeV. The HERA data points are consistent with those from TASSO [39] data and a clear agreement in the rate of growth of the HERA points with the e⁺e^- data [39,40] is observed.

  

Figure:  as a function of Q. The HERA data are compared to results from OPAL, TASSO and TOPAZ. A straight line fit of the form $\mbox{$\xi_{\rm peak}$}~=~b~ln(Q)~+~c$to the ZEUS  values is indicated as well as the line corresponding to b = 1, discussed in the text.

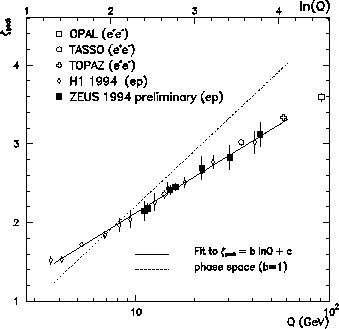The increase of  can be approximated phenomenologically by the straight line fit $\mbox{$\xi_{\rm peak}$}\;=\; b\: \ln(Q)+c$also shown in figure 7. Also shown is the statistical fit to the data when b=1 which would be the case if the QCD cascade was of an incoherent nature, dominated by cylindrical phase space. (A discussion of phase space effects is given in [41].) In such a case, the logarithmic particle momentum spectrum would be peaked at a constant value of momentum, independent of Q. The observed gradient is clearly inconsistent with b=1 and therefore inconsistent with cylindrical phase space thus supporting the coherent nature of gluon radiation.