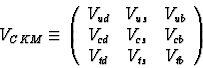
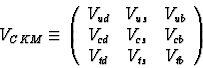 |
(1) |
The CKM matrix is unitary ie ![]() which
leads to 9 unitarity conditions expressed in terms of the matrix elements.
There are several (approximate)
parameterisations of the CKM matrix, one of the more
popular approaches is that of Wolfenstein [2],
eqn(2), where the matrix elements are expressed in terms
of powers of
which
leads to 9 unitarity conditions expressed in terms of the matrix elements.
There are several (approximate)
parameterisations of the CKM matrix, one of the more
popular approaches is that of Wolfenstein [2],
eqn(2), where the matrix elements are expressed in terms
of powers of ![]() where
where ![]() is the Cabibbo angle.
As can be seen from this parameterisation, the
9 complex elements of the matrix can be expressed in terms of 4 independent
variables; three real parameters
is the Cabibbo angle.
As can be seen from this parameterisation, the
9 complex elements of the matrix can be expressed in terms of 4 independent
variables; three real parameters ![]() and an
imaginary part of a complex number,
and an
imaginary part of a complex number, ![]() The 18 parameters of the CKM matrix can be reduced to 4 because of the
unitarity constraints and the arbitrary nature of the relative quark
phases [3].
It is the complex phase in the VCKM that leads to CP
violation in the standard model.
The 18 parameters of the CKM matrix can be reduced to 4 because of the
unitarity constraints and the arbitrary nature of the relative quark
phases [3].
It is the complex phase in the VCKM that leads to CP
violation in the standard model.
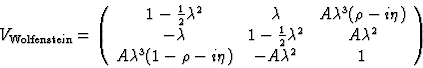 |
(2) |
The unitarity condition
VudVub* + VcdVcb* + VtdVtb* = 0
is of particular interest since
The non-closure of this
triangle ie ![]() would suggest that our
understanding of CP violation within the Standard Model was incomplete.
Physics beyond the Standard Model can be further investigated, for example,
by measuring CP asymmetries in several B decays that depend on the
same unitarity angle or studying decays where zero asymmetries are
expected in the Standard Model.
would suggest that our
understanding of CP violation within the Standard Model was incomplete.
Physics beyond the Standard Model can be further investigated, for example,
by measuring CP asymmetries in several B decays that depend on the
same unitarity angle or studying decays where zero asymmetries are
expected in the Standard Model.
CP violation in the B system should be observable through the phenomenon
of ![]() mixing, see for example [4]. This
mixing, see for example [4]. This ![]() mixing is dominated by box-diagrams with virtual
mixing is dominated by box-diagrams with virtual ![]() fig 2.
fig 2.
The following decays
are into a CP eigenstate.
If this is coupled with only a single diagram
contributing to the decay, CP asymmetries can be constructed which are
directly related to the angles of the unitarity triangle. For example,
these conditions occur
for the decay mode ![]() Here the number of B0d which decay at time t (where t is
expressed in units of lifetime) is proportional to
Here the number of B0d which decay at time t (where t is
expressed in units of lifetime) is proportional to
| |
(3) |
| |
(4) |
![]()
By
integrating eqns. (4) and (5)
over time a similar asymmetry can be constructed which is
proportional to
![]() . (Although
for coherent B production ie the
. (Although
for coherent B production ie the ![]() pair is produced in a definite CP state, this time
integrated asymmetry is zero.)
In addition this channel is experimentally very promising
because of the dilepton decay of the
pair is produced in a definite CP state, this time
integrated asymmetry is zero.)
In addition this channel is experimentally very promising
because of the dilepton decay of the ![]() Unfortunately additional decay diagrams contribute to the other
channels listed in eqn(3)
so there is no longer a complete cancellation of
the hadronic matrix elements in the CP asymmetry. The
Unfortunately additional decay diagrams contribute to the other
channels listed in eqn(3)
so there is no longer a complete cancellation of
the hadronic matrix elements in the CP asymmetry. The ![]() channel, which is dependent on the angle
channel, which is dependent on the angle
![]() is predicted to have large hadronic corrections from
`penguin' diagrams, fig. 3. The
is predicted to have large hadronic corrections from
`penguin' diagrams, fig. 3. The ![]() (dependent on the angle
(dependent on the angle ![]() ) also has
additional hadronic contributions but, in addition, suffers from
a very low branching fraction. Fortunately
there are, of course, many other channels which can be used to measure
CP violation, eg see ref. [5].
) also has
additional hadronic contributions but, in addition, suffers from
a very low branching fraction. Fortunately
there are, of course, many other channels which can be used to measure
CP violation, eg see ref. [5].
latex2html conversion by www person on 1997-10-22