


Next: Improved Cherenkov angle resolutions
Up: Cherenkov angle reconstruction
Previous: Cherenkov angle reconstruction
The small number of Cherenkov photons from the aerogel, and the
absence of the silicon telescope in Configuration 1, prevents use of
the improved resolution fitting methods detailed in
Section 7.2. In the absence of any beam trajectory
information, beyond that implied by the scintillator acceptance, this
method is applied directly to data, using the nominal (0, 0, - 1) beam
direction. It serves as a cross-check to allow comparisons
with more precise determinations explained later. These ``raw''
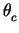 distributions are shown in Figure 12
for the case of Configuration 2 with 1 m of
C4F10.
distributions are shown in Figure 12
for the case of Configuration 2 with 1 m of
C4F10.
Figure:
Raw Cherenkov angle distributions for hits detected in
each of the outer HPD detectors. The x axes units are in
milliradians.
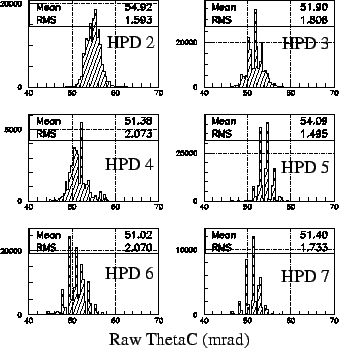 |
The pixellated nature of the HPD is apparent, as it induces a
multi-peak structure of the 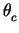 distribution. In
addition, there is a shift in the mean
distribution. In
addition, there is a shift in the mean 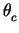 , and a clear
reduction in the raw resolutions for orientations of HPDs 2
and 5 where the Cherenkov ring lies parallel to a single row of
pixels.
, and a clear
reduction in the raw resolutions for orientations of HPDs 2
and 5 where the Cherenkov ring lies parallel to a single row of
pixels.
Raw Cherenkov resolutions are determined from data using HPDs
(2,3,5,6), without filters, in Figure 12, and
which average
1.76 mrad. The RMS of the observed
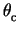 distribution is used as an estimate of the width, as pixellisation
effects makes the distributions difficult to interpret using Gaussian
fits. Similarly, the raw
distribution is used as an estimate of the width, as pixellisation
effects makes the distributions difficult to interpret using Gaussian
fits. Similarly, the raw 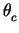 distributions are determined for
runs taken with aerogel in Configuration 1. The measured
RMS values of the raw Cherenkov resolutions
average
4.78 mrad for HPDs (2,3,5,6). No aerogel data was
collected using Configuration 2.
distributions are determined for
runs taken with aerogel in Configuration 1. The measured
RMS values of the raw Cherenkov resolutions
average
4.78 mrad for HPDs (2,3,5,6). No aerogel data was
collected using Configuration 2.
Simulation is used to determine resolution contributions due to
chromatic aberration, discrete pixel sizes and the emission point
uncertainty. The input beam trajectory uncertainty for this
configuration is that implied by the trigger scintillator acceptance.
The expected contributions are summarised in Table 6
and, when added in quadrature, total
1.72 mrad for
C4F10 and
3.20 mrad for silica aerogel.
Table 6:
Summary of expected resolution
contributions for the analysis of the Cherenkov angles using
the nominal beam direction for
C4F10 without
aerogel, with a mylar window, and and silica
aerogel in Configurations 2 and 1 respectively.
| |
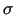 ( (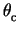 ) (mrad) ) (mrad) |
| Contribution Source |
C4F10 |
Aerogel |
| Pressure Variation |
0.70 |
0.70 |
| Emission Point Error |
0.58 |
0.66 |
| Chromatic Aberration |
1.03 |
1.06 |
| Finite Pixel Size |
0.56 |
2.73 |
| Beam Trajectory Error |
0.87 |
0.87 |
| Total in Quadrature |
1.72 |
3.20 |
|
The aerogel Cherenkov angle resolution is dominated by the finite
pixel size, because of the shorter focal length mirror used in
Configuration 1. The agreement between observed and expected raw
resolutions is reasonable considering systematic uncertainties due to
estimating the widths of the discretised distributions.
In order to improve the Cherenkov angle resolution, it is
necessary to reduce the dominant contributions listed in
Table 6. Effects of radiator pressure variation are
reduced by deactivating the recirculation system, and measuring the
mean Cherenkov angles in blocks of events recorded sequentially in
time. Extrapolating the observed time variation of the reconstructed
Cherenkov angles allows remaining uncertainties to be extracted from
data. The chromatic aberration contribution is reduced for HPDs (4,7) by using mylar filters to prevent photons with
wavelengths below
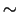 350 nm from entering the HPD
photo-cathode. The beam trajectory is estimated more accurately using
two methods:
350 nm from entering the HPD
photo-cathode. The beam trajectory is estimated more accurately using
two methods:
- Silicon telescope data, when available, allows precise
constraints on the input particle trajectory. A single specific
pixel, on each of the three silicon planes, is demanded as being hit
for the beam vector to be used5.
- Geometrical reconstruction uses an elliptical fit
to events with
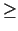 4 hit pixels from each of HPDs (2,3,5,6)
and (4,7). The centre of each ellipse is used to estimate the beam
trajectory for the Cherenkov angle reconstruction on that HPD.
A vector, connecting the ellipse centre to the mirror centre, is
reflected in the mirror to give an estimate of the incoming beam
direction. Systematic checks are necessary to ensure the fit procedure
does not bias the results. Resolution contribution from uncertainties
in the beam trajectory can be determined from the observed error
distributions from the fit. They correspond to values of 0.28 mrad
for HPDs (2,3,5,6) and 0.58 mrad for HPDs(4,7).
4 hit pixels from each of HPDs (2,3,5,6)
and (4,7). The centre of each ellipse is used to estimate the beam
trajectory for the Cherenkov angle reconstruction on that HPD.
A vector, connecting the ellipse centre to the mirror centre, is
reflected in the mirror to give an estimate of the incoming beam
direction. Systematic checks are necessary to ensure the fit procedure
does not bias the results. Resolution contribution from uncertainties
in the beam trajectory can be determined from the observed error
distributions from the fit. They correspond to values of 0.28 mrad
for HPDs (2,3,5,6) and 0.58 mrad for HPDs(4,7).
The results from data and simulated expectations are summarised
separately for the two types of improved beam direction
estimates.



Next: Improved Cherenkov angle resolutions
Up: Cherenkov angle reconstruction
Previous: Cherenkov angle reconstruction
latex2html conversion by www person on 2000-01-23


![]() distribution is used as an estimate of the width, as pixellisation
effects makes the distributions difficult to interpret using Gaussian
fits. Similarly, the raw
distribution is used as an estimate of the width, as pixellisation
effects makes the distributions difficult to interpret using Gaussian
fits. Similarly, the raw ![]() distributions are determined for
runs taken with aerogel in Configuration 1. The measured
RMS values of the raw Cherenkov resolutions
average
4.78 mrad for HPDs (2,3,5,6). No aerogel data was
collected using Configuration 2.
distributions are determined for
runs taken with aerogel in Configuration 1. The measured
RMS values of the raw Cherenkov resolutions
average
4.78 mrad for HPDs (2,3,5,6). No aerogel data was
collected using Configuration 2.
![]() 350 nm from entering the HPD
photo-cathode. The beam trajectory is estimated more accurately using
two methods:
350 nm from entering the HPD
photo-cathode. The beam trajectory is estimated more accurately using
two methods: