


Next: Cherenkov angle resolutions for
Up: Performance of a Prototype
Previous: Discussion and detector response
Cherenkov angle reconstruction
Individual HPD hits are used to determine
Cherenkov angles. The aim is to reconstruct the precision with which
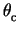 is determined for single photons. The observed
resolution in data is then compared with that expected from the
simulation described in Section 5. Data are
used where four HPDs, (2,3,5,6), have no filter in front of their
input windows, but where two HPDs, 4 & 7, have mylar filters.
The method used to reconstruct Cherenkov angles in data is illustrated
in Figure 11 and requires the following parameters to
be determined :
is determined for single photons. The observed
resolution in data is then compared with that expected from the
simulation described in Section 5. Data are
used where four HPDs, (2,3,5,6), have no filter in front of their
input windows, but where two HPDs, 4 & 7, have mylar filters.
The method used to reconstruct Cherenkov angles in data is illustrated
in Figure 11 and requires the following parameters to
be determined :
Figure 11:
Schematic of the Cherenkov angle reconstruction in the
tilted spherical mirror geometry.
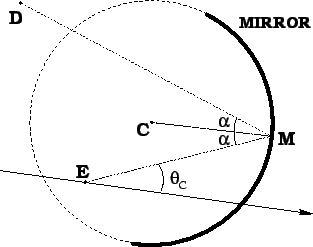 |
- The detection point, D supplied by the
physical hit position on the surface of the HPD,
subject to alignment uncertainties.
- The centre of curvature of the mirror, C,
defined by the measured focal length and the rotation angle relative
to the nominal beam direction. The focal length has a precision of
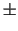 10 mm, whereas the rotation angle is nominally
18 degrees, but is subject to small uncertainties when centering the
ring image on the detector plane using micrometer screws.
10 mm, whereas the rotation angle is nominally
18 degrees, but is subject to small uncertainties when centering the
ring image on the detector plane using micrometer screws.
- The direction of the particle through the system determined
using, either the nominal direction, (0, 0, - 1), or
an improved estimator, such as from the silicon telescope or
event-by-event reconstruction.
- The emission point, E, of the photon is assumed
to be the centre of the radiator, traversed by the particle. This is
the position which minimises systematic uncertainties.
The reflection point, M, is constrained to lie on the same plane as
E, D and C. The two-dimensional problem is
solved [11] for 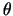 under the condition that incident and
reflected angles (
under the condition that incident and
reflected angles (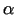 ) are equal.
) are equal.
Subsections



Next: Cherenkov angle resolutions for
Up: Performance of a Prototype
Previous: Discussion and detector response
latex2html conversion by www person on 2000-01-23
