Drift of charge carriers

The initial distribution of charge is assumed to be uniform along the linear track of a minimum ionizing particle. Genaration of delta rays and charge spreading has not yet been implemented, but is assumed to be not essential at the present stage. A constant number of electron-hole pairs is generated for each track. A time-slice approach is used in simulation, as a current signal is required. Each individual carrier is followed during its drift. Trapping probabilities are calculated from the trap concentrations , N_k, cross sections and drift velocity v(x(t)). A flag associated with each carrier indicates its status, which can be: free, trapped, reached the electrode. The probability of being trapped by the k^th type of trap is given by:

where is the time step.

 
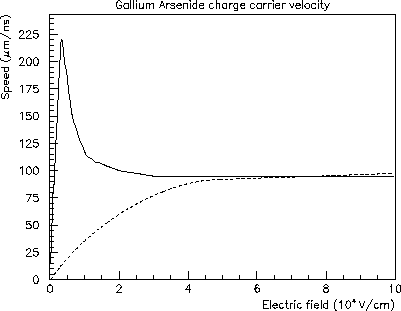
Figure 4: Electron and hole drift speed used in the program. The saturation velocity is nearly the same for electrons and holes in this material.  

Detrapping is also taken into account as a possible process. We assume that there is a mean trapped time and that both and are independent of electric field.

The carrier drift velocity is calculated from the electric field using parametrizations of the experimental data [14][15], as shown in fig. 4. We note that provided the field is high enough, the details of its shape have a negligible influence on carrier velocity for the larger part of the device, as saturation is reached. If drift in a magnetic field and diffusion have to be considered, however, an exact knowledge of the electric field is essential.

 
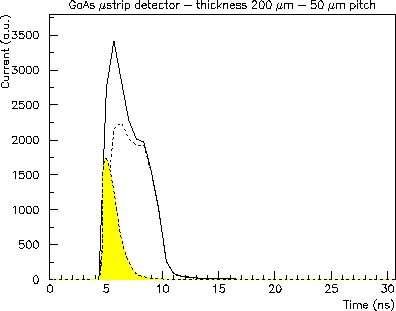
Figure: An example of the simulated current signal generated by minimum ionizing particles traversing a thick detector in the middle of the considered strip, which in this case is wide. The bias voltage was 180 V. The major contribution is due to holes which approach the area where the weighting field is high. The electron contribution is shown in the shaded curve.  

The current signal on the j^th electrode is calculated from the Ramo-Shockley theorem:

where N_c is twice the number of electron-hole pairs generated, is the weighting field and q_n the charge of the carrier. The charge signal is obtained by integration of i(t) and gives the charge collection efficiency. An example of a current signal is shown in fig. 5 and is used as input for SPICE.