![\begin{figure}
\epsfxsize=8.cm
\centering
\leavevmode
\epsfbox[49 147 520 645]{mcmix.ps}\end{figure}](img174.gif) |
![\begin{figure}
\epsfxsize=8.cm
\centering
\leavevmode
\epsfbox[49 147 520 645]{mcmix.ps}\end{figure}](img174.gif) |
![\begin{figure}
\epsfxsize=8.cm
\centering
\leavevmode
\epsfbox[105 240 445 585]{method_mx.eps}\end{figure}](img176.gif) |
One of the major uncertainties comes from the estimation of the various contributions to the cross-section which depends on Monte Carlo techniques. This problem has been addressed in a different way in the ZEUS analysis [23]. Here, the mass spectrum, MX2, is measured as a function of W and Q2, as shown in Fig. 15 for a representative interval, where the measured mass is reconstructed in the calorimeter and corrected for energy loss but not for detector acceptance, resulting in the turnover at large MX2. The diffractive data are observed as a low mass shoulder at low MX2. which becomes increasingly apparent at higher W. Also shown in the figure are the estimates of the non-diffractive contribution based on a direct fit to the data, discussed below.
The probability of producing a gap is exponentially suppressed
as a function of the rapidity gap, and hence as a function of ![]() ),
for non-diffractive interactions. The slope of this exponential
is directly related to the height of the plateau distribution of
multiplicity in the region of rapidity where the subtraction is made.
The data can thus be fitted to functions of the form
),
for non-diffractive interactions. The slope of this exponential
is directly related to the height of the plateau distribution of
multiplicity in the region of rapidity where the subtraction is made.
The data can thus be fitted to functions of the form
![]() ,
in the region where the detector acceptance is uniform,
where b, C and D are determined from the fits.
Here, D represents a first-order estimate of the diffractive contribution
which is approximately flat in
,
in the region where the detector acceptance is uniform,
where b, C and D are determined from the fits.
Here, D represents a first-order estimate of the diffractive contribution
which is approximately flat in ![]() ).
The parameter which determines the background is b.
In general the measured value of b is incompatible with that of the
ARIADNE Monte Carlo.
This result in itself is interesting, since the fact that ARIADNE approximately
reproduces the observed forward ET (
).
The parameter which determines the background is b.
In general the measured value of b is incompatible with that of the
ARIADNE Monte Carlo.
This result in itself is interesting, since the fact that ARIADNE approximately
reproduces the observed forward ET (![]() multiplicity) flow but does not
reproduce the measured value of b suggests that significantly different
correlations of the multiplicities are present in non-diffractive DIS
compared to the Monte Carlo expectations.
This method enables a diffractive cross-section to be determined
directly from the data at the expense of being limited in the range of large
masses that can analysed.
multiplicity) flow but does not
reproduce the measured value of b suggests that significantly different
correlations of the multiplicities are present in non-diffractive DIS
compared to the Monte Carlo expectations.
This method enables a diffractive cross-section to be determined
directly from the data at the expense of being limited in the range of large
masses that can analysed.
Finally,
the advent of the leading proton spectrometers (LPS) at HERA is especially
important in these diffractive measurements, since internal
cross-checks of the measurements as a function of t, M2, W2 and Q2
can be performed
and underlying assumptions can be studied experimentally. Only in these
measurements can we positively identify the diffracted proton and hence
substantially reduce uncertainties on the non-diffractive and double
dissociation backgrounds.
This is illustrated in Fig. 16, where the xL (where
xL = p'/p)
distribution includes a clear diffractive peak for
![]() .
It should be noted, however, that the contribution from other Reggeon
exchanges cannot be neglected until
.
It should be noted, however, that the contribution from other Reggeon
exchanges cannot be neglected until
![]() (in fact the
result at lower xL can be simply interpreted via reggeon
(approximated by pion) exchange, as discussed below.)
However, new experimental uncertainties are introduced
due to the need for precise
understanding of the beam optics and relative alignment of the detectors.
Reduced statistical precision also results due to the limited
geometrical acceptance of the detectors (
(in fact the
result at lower xL can be simply interpreted via reggeon
(approximated by pion) exchange, as discussed below.)
However, new experimental uncertainties are introduced
due to the need for precise
understanding of the beam optics and relative alignment of the detectors.
Reduced statistical precision also results due to the limited
geometrical acceptance of the detectors (![]() 6%).
6%).
![\begin{figure}
\vspace{1cm}
\epsfxsize=8.cm
\centering
\leavevmode
\epsfbox[95 350 485 550]{method_xl.ps}\end{figure}](img181.gif) |
![\begin{figure}
\vspace{1cm}
\centering
\mbox{
\subfigure[$t$\space distribution...
...on $W^2$ ]
{\psfig{figure=zeus_tchapin.ps,width=.45\textwidth} }
}
\end{figure}](img182.gif) |
Photoproduction Results:
ZEUS has measured the photon dissociation t distribution using the LPS,
as shown in Fig. 17.
An exponential fit to the data yields a b-slope
parameter,
![]() GeV-2. A comparison of the data
with lower W data from Chapin et al. shows that the result is consistent
with shrinkage, as previously
discussed in relation to exclusive
GeV-2. A comparison of the data
with lower W data from Chapin et al. shows that the result is consistent
with shrinkage, as previously
discussed in relation to exclusive ![]() production.
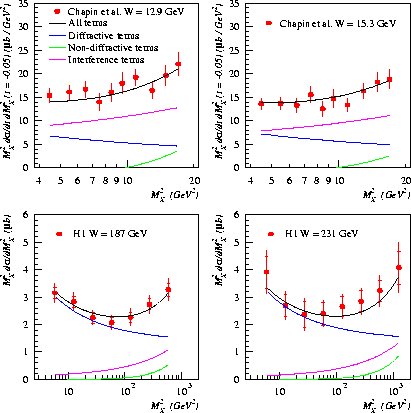
H1 results on the photon dissociation cross-sections as a function of
MX2 in two W intervals are shown in Fig. 18.
Regge theory predicts the form of
the cross-section as a function of MX and W, as discussed with respect
to proton dissociation. The cross-section is therefore fitted to the form
production.
H1 results on the photon dissociation cross-sections as a function of
MX2 in two W intervals are shown in Fig. 18.
Regge theory predicts the form of
the cross-section as a function of MX and W, as discussed with respect
to proton dissociation. The cross-section is therefore fitted to the form
 |
Deep inelastic structure of diffraction:
A new era for diffraction was opened with the study of the dissociation
of virtual photons.
Here, the photon can be considered as probing the structure of the
exchanged colourless object mediating the interaction.
The deep inelastic structure of colour singlet exchange is therefore being
studied.
In the presentation of the results, the formalism changes [24],
reflecting an assumed underlying partonic description,
and two orthogonal variables are determined
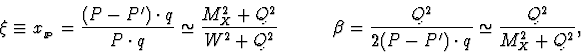
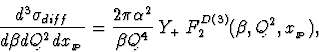
In addition to the structure of the pomeron, corresponding to large xL,
it is also possible to study the structure of the reggeons that contribute
at lower xL. H1 has analysed the leading proton data at lower xL
(
0.7<xL<0.9) and employed the formalism noted above to measure the
structure of the exchange for reasonably forward protons, as
shown in Fig. 19 [25].
The data are consistent with a flat ![]() dependence in all intervals
of
dependence in all intervals
of ![]() and Q2 i.e.
and Q2 i.e.
![]() .
This is consistent with a factorisable ansatz of
.
This is consistent with a factorisable ansatz of
![]() where
where
![]() measures the flux of reggeons in the proton
and
measures the flux of reggeons in the proton
and
![]() is the probed structure of these reggeons.
The exponent of
is the probed structure of these reggeons.
The exponent of ![]() is identified as
is identified as
![]() ,
where
,
where
![]() measures the effective
measures the effective ![]() dependence
(
dependence
(
![]() dependence at fixed MX2 and Q2) of the cross-section,
integrated over t.
The data are consistent with
dependence at fixed MX2 and Q2) of the cross-section,
integrated over t.
The data are consistent with
![]() ,
corresponding to
,
corresponding to
![]() .
These data involve colour singlet exchange and need to be
explained in terms of QCD, but they are clearly not of a
diffractive nature.
.
These data involve colour singlet exchange and need to be
explained in terms of QCD, but they are clearly not of a
diffractive nature.
The area of interest for diffraction is in the behaviour of small values of
![]() ,
where
,
where ![]() is now identified as
is now identified as
![]() .
Here, the data fall approximately as
.
Here, the data fall approximately as
![]() (equivalent to a flat cross-section with increasing W) and
therefore the data are plotted as
(equivalent to a flat cross-section with increasing W) and
therefore the data are plotted as
![]() in
Fig. 20.
In the H1 case, the measurement is presented with no explicit
subtraction for the non-diffractive contribution and quoted for limited
masses of the dissociated proton system (MN < 1.6 GeV). The measurement
relies upon a good understanding of the various contributions to the
cross-section in and around the measured region: the control plots in
Fig. 14
illustrate how well this is achieved by combining the different Monte
Carlo contributions.
in
Fig. 20.
In the H1 case, the measurement is presented with no explicit
subtraction for the non-diffractive contribution and quoted for limited
masses of the dissociated proton system (MN < 1.6 GeV). The measurement
relies upon a good understanding of the various contributions to the
cross-section in and around the measured region: the control plots in
Fig. 14
illustrate how well this is achieved by combining the different Monte
Carlo contributions.
Fits of the form
![]() are performed
where the normalisation constants
are performed
where the normalisation constants
![]() are allowed to differ
in each
are allowed to differ
in each ![]() interval.
The fits are motivated by the factorisable ansatz of
interval.
The fits are motivated by the factorisable ansatz of
![]() where
where
![]() measures the flux of pomerons in the proton
and
measures the flux of pomerons in the proton
and
![]() is the probed structure of the pomeron.
The exponent of
is the probed structure of the pomeron.
The exponent of
![]()